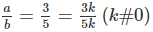Gọi hai số cần tìm là a và b \(\left(a\ne0\right)\)
Ta có : \(\dfrac{a}{b}=\dfrac{3}{5}=\dfrac{3k}{5k}\left(k\ne0\right)\)
Vậy \(a=3k , b=5k\) ,do đó :
\(a^2-b^2=\left(3k\right)^2-\left(5k\right)^2=-64\)
\(9k^2-25k^2=-64\)
\(-16k^2=-64\)
\(k^2=4\)
\(k=\pm2.\)
Với \(k=2\) thì \(a=3.1=6,b=5.2=10\)
Với \(k=-2\) thì \(a=3.\left(-2\right)=-6,b=5.\left(-2\right)=-10\)
Gọi hai số phải tìm là a và b (b ≠ 0)
Ta có
Vậy a = 35; b = 5k, do đó:
a2 - b2 = (3k)2 - (5k)2 = -64
⇔9k2 - 25k2 = -64
⇔-16k2 = -64
⇔k2 = 4
⇔k = -2 hoặc k = 2
Với k = 2 thì a = 3.2 = 6; b = 5.2 = 10
Với k = -2 thì a = 3.(-2) = -6; b = 5.(-2) = 10
Gọi hai số phải tìm là a và b (b ≠ 0)
Ta có
Vậy a = 35; b = 5k, do đó:
a2 - b2 = (3k)2 - (5k)2 = -64
⇔9k2 - 25k2 = -64
⇔-16k2 = -64
⇔k2 = 4
⇔k = -2 hoặc k = 2
Với k = 2 thì a = 3.2 = 6; b = 5.2 = 10
Với k = -2 thì a = 3.(-2) = -6; b = 5.(-2) = 10