Đặt một cạnh góc vuông là x (x > 0) thì cạnh còn lại là \(\sqrt {25 - {x^2}} \)
Diện tích tam giác vuông là: \(f(x) = \frac{{1}}{2} x\sqrt {25 - {x^2}} \)
Tập xác định: \(D = (0; 5 )\)
\(f'(x) = \frac{{1}}{2}\sqrt {25 - {x^2}} - \frac{{1}}{2}. \frac{{{x^2}}}{{\sqrt {25 - {x^2}} }}\)
Tập xác định mới: \({D_1} = (0; 5 )\)
\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\sqrt {2} }}{2}\\x = - \frac{{5\sqrt {2} }}{2}(loại)\end{array} \right.\)
Bảng biến thiên:
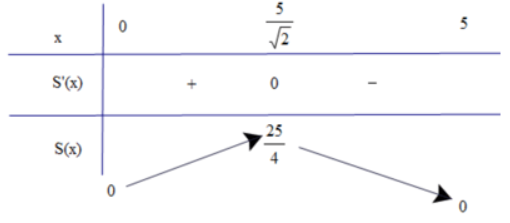
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_D f(x) = f(\frac{{5\sqrt {2} }}{2}) = \frac{25}{4}\).
Vậy diện tích lớn nhất của tam giác là \(\frac{25}{4}\).
Đúng 0
Bình luận (0)

