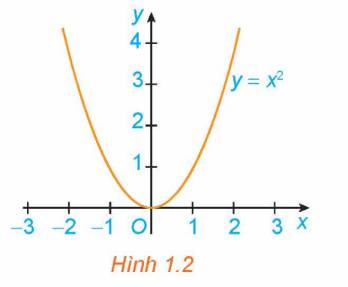
Từ đồ thị ta thấy:
+ Xét khoảng \(\left( {0; + \infty } \right)\): \(\forall {x_1},{x_2} \in \left( {0; + \infty } \right),{x_1} < {x_2}\) thì \(x_1^2 < x_2^2\) hay \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Suy ra, hàm số \(y = {x^2}\) đồng biến trên \(\left( {0; + \infty } \right)\).
+ Xét khoảng \(\left( { - \infty ;0} \right)\): \(\forall {x_1},{x_2} \in \left( { - \infty ;0} \right),{x_1} < {x_2}\) thì \(x_1^2 > x_2^2\)hay \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Suy ra, hàm số \(y = {x^2}\) nghịch biến trên \(\left( { - \infty ;0} \right)\).
Đúng 0
Bình luận (0)