Trong thực tiễn có nhiều ví dụ minh họa cho mặt phẳng. Chẳng hạn: tấm gương phẳng, mặt bàn, mặt bảng… Cho ta hình ảnh một phần mặt phẳng trong không gian
Trong Ví dụ 4, xác định giao tuyến của hai mặt phẳng (SAC) và (SBD).
Hình 15 mô tả một phần của phòng học. Nếu coi bức tường chứa bảng và sàn nhà là hình ảnh của hai mặt phẳng thì giao của hai mặt phẳng đó là gì?
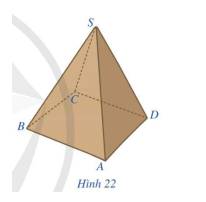
Hình 22 là hình ảnh của một hộp quà lưu niệm có dạng hình chóp tứ giác đều S.ABCD. Quan sát Hình 22 và trả lời các câu hỏi:
a) Đỉnh S có nằm trong mặt phẳng (ABCD) hay không?
b) Mỗi mặt của hộp quà lưu niệm có dạng hình gì?
Quan sát Hình 1, nếu coi mặt sân Napoleon là một phần của mặt phẳng (P) thì đỉnh của kim tự tháp có thuộc mặt phẳng (P) hay không?
Hình 25 là hình nhr của khối rubik tam giác (Pyramix). Quan sát Hình 25 và trả lời các câu hỏi:
a) Khối rubik tam giác có bao nhiêu đỉnh? Các đỉnh có cùng nằm trong một mặt phẳng không?
b) Khối rubik tam giác có bao nhiêu mặt? Mỗi mặt của khối rubik tam giác là những hình gì?
Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.
a) Xác định giao điểm của CD với hai mặt phẳng (SAB) và (SCD)
b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD)
c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC)
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và AD.
a) Xác định giao điểm của mặt phẳng (CMN) với các đường thẳng AB, SB
b) Xác định giao tuyến của mặt phẳng (CMN) với mỗi mặt phẳng (SAB) và (SBC)
Trong mặt phẳng (P) cho tam giác ABC. Điểm D không thuộc mặt phẳng (P). Hỏi qua hai đường thẳng AD và BC có xác định được một mặt phẳng không?
Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho \(MA = 2MS,NS = 2NC\)
a) Xác định giao điểm của MN với mặt phẳng (ABC)
b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC)