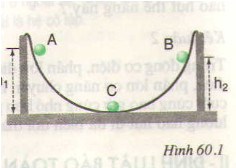
Vì trượt không ma sát, ta có thể sử dụng định luật bảo toàn cơ năng.
Chọn gốc tính thế năng tại chân mặt phẳng nghiêng (mpn)
Cơ năng tại đỉnh của mpn là:
W= \(\frac{1}{2}mv^2+mgh\)
Cơ năng tại chân của mpn là:
W'= \(\frac{1}{2}mv'^2\)
Định luật bảo toàn cơ năng:
W=W'
<=> \(\frac{1}{2}\cdot2^2+10\cdot1,6\)= \(\frac{1}{2}v'^2\)
=> v'= 6(m/s)
Vậy...