TH1: Cạnh bên bằng 30 cm
Khi đó cạnh đáy bằng: 120 – (30 + 30 ) =60 (cm)
Vì 30 + 30 = 60 nên bộ 3 độ dài này không tạo được thành tam giác.
TH2: Cạnh đáy bằng 30 cm
Khi đó cạnh bên bằng: (120 – 30) : 2 = 45 (cm)
Đánh dấu AB = CD = 45 cm.
TH1: Cạnh bên bằng 30 cm
Khi đó cạnh đáy bằng: 120 – (30 + 30 ) =60 (cm)
Vì 30 + 30 = 60 nên bộ 3 độ dài này không tạo được thành tam giác.
TH2: Cạnh đáy bằng 30 cm
Khi đó cạnh bên bằng: (120 – 30) : 2 = 45 (cm)
Đánh dấu AB = CD = 45 cm.
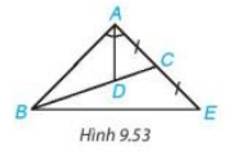
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD= 2 DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A
Gợi ý D là trọng tâm của tam gíac ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.
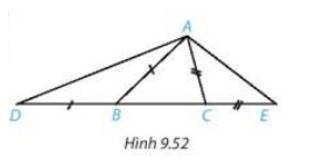
Cho tam giác ABC ( AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA ( H.9.52)
a) So sánh \(\widehat {ADE}\) và \(\widehat {AED}\).
b) So sánh các đoạn thẳng AD và AE.
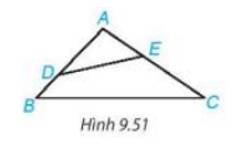
Cho tam giác ABC có \(\widehat {BAC}\) là góc tù. Lấy điểm D nằm giữa A và B, lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng
a)\(AI < \dfrac{1}{2}\left( {AB + AC} \right)\)
b)\(AM < \dfrac{1}{2}\left( {AB + AC} \right)\)