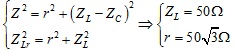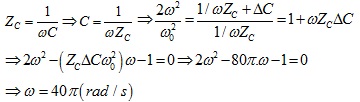Chủ đề / Chương

Bài học

Chủ đề

Cuộn dây không thuần cảm, cộng hưởng điện

Hãy tham gia nhóm Học sinh Hoc24OLM
TA

Một cuộn dây không thuần cảm nối tiếp với tụ điện có điện dung C thay đổi được trong mạch điện xoay chiều có điện áp u=U_{0}cos\omega t(V) . Ban đầu dung kháng ZC và tổng trở ZLr của cuộn dây và Z của toàn mạch đều bằng 100Ω. Tăng điện dung thêm một lượng \Delta C=0,125.10^{-3}/\pi (F) thì tần số dao động riêng của mạch này khi đó là 80\pi (rad/s). Tần số  ω của nguồn điện xoay chiều bằng

A. 40π (rad/s)                B. 100 π (rad/s)              C. 80π (rad/s)                 D. 50π (rad/s)

Lớp 12 Vật lý Cuộn dây không thuần cảm, cộng hưởng điện

Khách
 
DT
25 tháng 1 2016 lúc 22:09

Từ ĐK đầu bài ta có: Zc^{2}=r^{2}+Zl^{2}=r^{2}+(Zl-Zc)^{2}\Rightarrow Zc=2Zl=100\Rightarrow \omega ^{2}=\frac{1}{2LC}
tần số dao động riwwng của mạch là:(80\Pi )^{2}=\frac{1}{L(C-\Delta C)}\Rightarrow L.C-L\Delta C=\frac{1}{80^{2}.10}\Rightarrow \frac{1}{2\omega^{2}}-\frac{50}{\omega }.\frac{0,125.10^{-3}}{\Pi }=\frac{1}{80^{2}.10}
giải phương trình bâc 2 này ra ta được: \omega =40\Pi

Bình luận (0)
HD
25 tháng 1 2016 lúc 22:11

Z=Z_{C}=Z_{Lr}=100\Omega

Z_{C}=2Z_{L}\Rightarrow \frac{1}{\omega C}=2\omega L\Rightarrow \frac{1}{LC}=2\omega ^{2}(1)

{\omega _{0}}^{2}=\frac{1}{L(C+\Delta C)}(2)

Lấy (1) chia (2) ta được:  \frac{2\omega ^{2}}{{\omega _{0}}^{2}}=\frac{C+\Delta C}{C}

 

Bình luận (0)
Các câu hỏi tương tự
TH
1/đặt điện áp xoay chiều ổn định vào 2 đầu đoạn mạch mắc nối tiếp gồm cuộn dây có điện trở thuần R,có cảm kháng 150 và tụ điện có điện dung thay đổi được.Khi dung kháng Zc100 và Zc200 thì dòng điện trong mạch có pha ban đầu hơn kém nhau pi/4.Điện trở R bằng? 2/Xét mạch điện xoay chiều có tần số 50 mắc nt gồm R,cuộn cảm huần có cảm kháng 20 và tụ điện có điện dung Cthay đổi .Khi C ăng lên 5 lần so vs giá trị lúc cộng hưởng thì ddienj áp 2 đầu đoạn mạch và dòng điện lệch pha nhau pi/3.Giá trị R...
Đọc tiếp
Xem chi tiết
Lớp 12 Vật lý Cuộn dây không thuần cảm, cộng hưởng điện
MD
Cho mạch điện xoay chiều gồm một cuộn dây có hệ số tự cảm L  H và có điện trở thuần r 10 mắc nối tiếp với một tụ điện có điện dung   C  mF. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có tần số f 50Hz và điện áp hiệu dụng U 100V, pha ban đầu bằng 0. .Biểu thức của dòng điện qua mạch. Mọi ng giải chi tiết hô với 
Đọc tiếp
Xem chi tiết
Lớp 12 Vật lý Cuộn dây không thuần cảm, cộng hưởng điện
BN

Đoạn mạch xoay chiều gồm RLC măc nối tiếp, với R = 215,5, khi tần số dòng điện là 50 hz thì cảm kháng của cuộn cảm là ZL=156,25, ZC = 400. để công suất của mạch bằng 1 thì tần số của dòng điện bằng bao nhiêu

Xem chi tiết
Lớp 12 Vật lý Cuộn dây không thuần cảm, cộng hưởng điện
PP
Một đoạn mạch gồm tụ điện có điện dung C, điện trở thuần R, cuộn dây có điện trở trong r và hệ số tự cảm L mắc nối tiếp. Khi đặt vào hai đầu đoạn mạch hiệu điện thế  u Usqrt2cosomega t (V) thì dòng điện trong mạch có giá trị hiệu dụng là I. Biết cảm kháng và dung kháng trong mạch là khác nhau. Công suất tiêu thụ trong đoạn mạch này làA.U^2/(R + r).B.(r + R ) I^2.C.I^2R.D.UI.
Đọc tiếp
Xem chi tiết
Lớp 12 Vật lý Cuộn dây không thuần cảm, cộng hưởng điện
MD
Một đoạn mạch nối tiếp ABC gồm một tụ điện (đoạn AB) và một cuộn dây (đoạn BC). Khi tần số dòng điện xoay chiều qua mạch bằng 1000Hz người ta đo được các điện áp hiệu dụng UAB  2 V, UBC   V, UAC  1V và cường độ hiệu dụng I 10-3 A.Tìm điện trở r và độ tự cảm L của cuộn dây 
Đọc tiếp
Xem chi tiết
Lớp 12 Vật lý Cuộn dây không thuần cảm, cộng hưởng điện
PP

Một mạch điện xoay chiều AB gồm điện trở \(R = 15\Omega\) mắc nối tiếp với một cuộn dây có điện trở thuần r và độ tự cảm L. Biết điện áp hiệu dụng hai đầu R là 30V, hai đầu cuộn dây là 40V và hai đầu A, B là 50V. Công suất tiêu thụ trong mạch là

A.140W.

B.60W. 

C.160W.

D.40W.

Xem chi tiết
Lớp 12 Vật lý Cuộn dây không thuần cảm, cộng hưởng điện
PP

Mạch điện xoay chiều mắc nối tiếp  gồm cuộn dây và tụ. Đặt vào hai đầu mạch một hđt xoay chiều \(u=160\sqrt2\cos (100\pi t)(V)\) thì hđt hiệu dụng hai đầu cuộn dây và tụ là 120V và 200V. Xác định hệ số công suất của mạch.

A.0,8.

B.0,5.

C.0,75.

D.0,6.

Xem chi tiết
Lớp 12 Vật lý Cuộn dây không thuần cảm, cộng hưởng điện
KT

Mạch điện xoay chiều gồm một cuộn dây mắc nối tiếp với tui điện . Cuộn dây có điện trở r=30Ω, độ tự cảm L=\(\dfrac{0,4}{\pi}\) H, tụ điện có điện dung C . Biểu thức điện áp tức thời giữa hai đầu đoạn mạch là u=120cos100πt(V) . Với giá trị nào của C thì công suất tiêu thụ của mạch có giá trị cực đại và giá công suất cực đại bằng bao nhiêu ?

Xem chi tiết
Lớp 12 Vật lý Cuộn dây không thuần cảm, cộng hưởng điện
BS
Điều nào sau đây đúng khi nói về đoạn mạch điện xoay chiều khi có cuộn dây thuần cảm kháng
Xem chi tiết
Lớp 12 Vật lý Cuộn dây không thuần cảm, cộng hưởng điện