Một cái lều có dạng hình lăng trụ \(ABC.A'B'C'\) có cạnh bên \(AA'\)vuông góc với đáy (Hình 24). Cho biết \(AB = AC = 2,4m;BC = 2{\rm{ }}m;AA' = 3m\).
a) Tính góc giữa hai đường thẳng \(AA'\) và \(BC\); \(A'B'\) và \(AC\).
b) Tính diện tích hình chiếu vuông góc của tam giác \(ABB'\) trên mặt phẳng \(\left( {BB'C'C} \right)\).
tham khảo
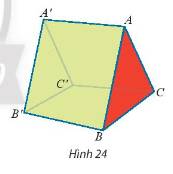
a) Vì \(AA'//BB'\) nên góc giữa \(AA'\) và \(BC\) là góc giữa \(BB'\) và \(BC\).
Vì cạnh bên vuông góc với đáy nên \(BB'\perp BC\). Do đó, \(\widehat{B'BC}=90^o\)
Vì \(A'B'//AB\) nên góc giữa \(A'B'\) và \(AC\) là góc giữa \(AB\) và \(AC\).
Ta có:\(\cos\widehat{BAC}=\dfrac{2,4^2+2,4^2-2^2}{2.2,4.2,4}=\dfrac{47}{72}\)
Nên \(\widehat{BAC}=49,2^o\)
b) Kẻ \(AH\perp BC\). Vì cạnh bên vuông góc với đáy nên \(BB'\perp AH\).
Ta có \(AH\perp BB',AH\perp BC\) nên \(AH\perp\left(BCC'B'\right)\).