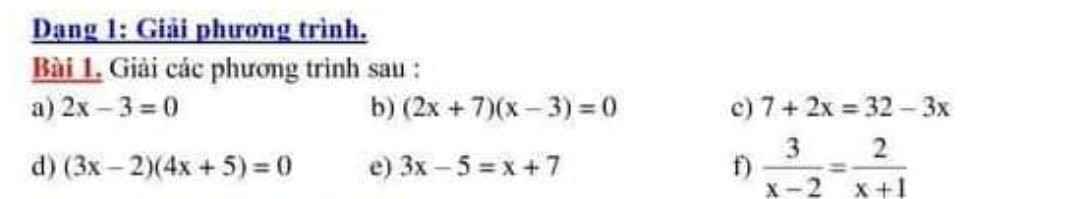ĐKXĐ:\(\left\{{}\begin{matrix}x\ne-\dfrac{7}{2}\\x\ne3\end{matrix}\right.\)
\(\dfrac{13}{2x^2+x-21}+\dfrac{1}{2x+7}=\dfrac{6}{x^2-9}\\ \Leftrightarrow\dfrac{13}{2x^2-6x+7x-21}+\dfrac{1}{2x+7}=\dfrac{6}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow\dfrac{13}{2x\left(x-3\right)+7\left(x-3\right)}+\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(2x+7\right)\left(x+3\right)}-\dfrac{6\left(2x+7\right)}{\left(x-3\right)\left(x+3\right)\left(2x+7\right)}=0\)
\(\Leftrightarrow\dfrac{13\left(x+3\right)}{\left(2x+7\right)\left(x-3\right)\left(x+3\right)}+\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(2x+7\right)\left(x+3\right)}-\dfrac{6\left(2x+7\right)}{\left(x-3\right)\left(x+3\right)\left(2x+7\right)}=0\)
\(\Leftrightarrow\dfrac{13x+39+x^2-9-12x-42}{\left(2x+7\right)\left(x-3\right)\left(x+3\right)}=0\)
\(\Rightarrow x^2+x-12=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=-4\left(tm\right)\end{matrix}\right.\)
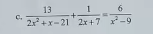



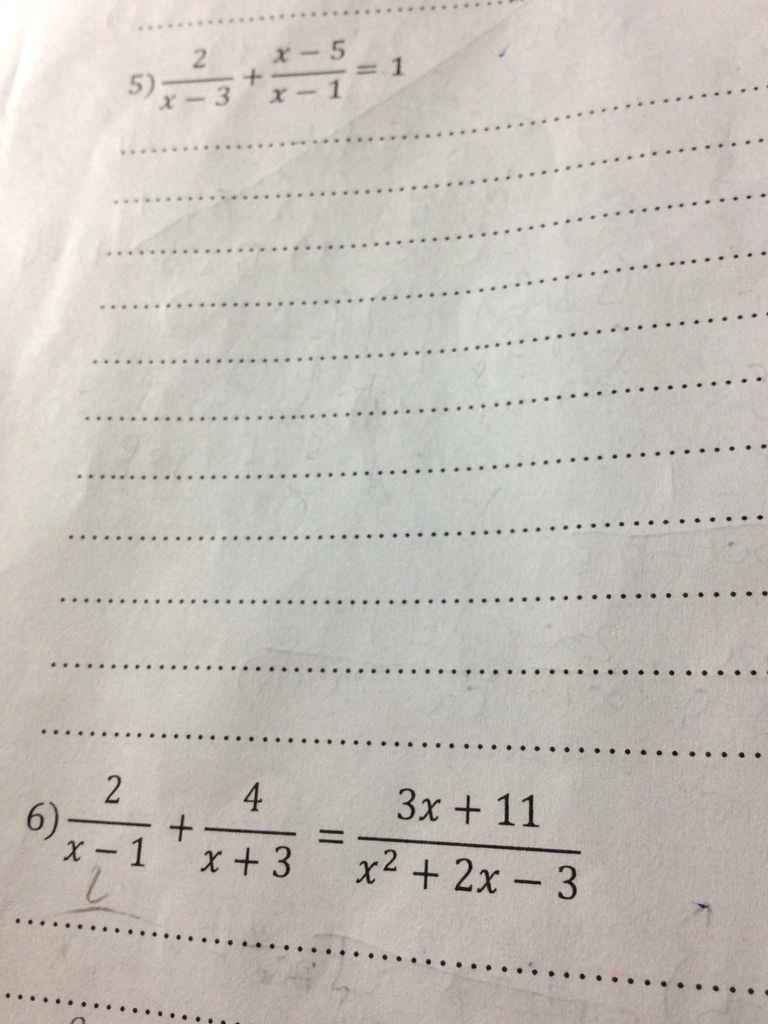 Giúp mình thêm 2 câu này cực gấp luôn nha cảm ơn
Giúp mình thêm 2 câu này cực gấp luôn nha cảm ơn