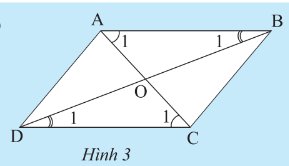
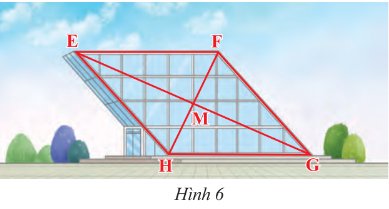
Do tứ giác EFGH là hình bình hành \(\Rightarrow\left\{{}\begin{matrix}HG=EF=40m\\HF=2HM=2\cdot16=32m\\EG=2EM=2\cdot36=72m\end{matrix}\right.\)
Bài 4. Hình bình hành - Hình thoi
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Một tứ giác có chu vi là \(52\) cm và một đường chéo là \(24\)cm. Tính độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.
Một tứ giác có chu vi là \(52\) cm và một đường chéo là \(24\)cm. Tính độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.
Tính độ dài cạnh của các khuy áo hình thoi có độ dài hai đường chéo lần lượt là ${3,2}$cm và ${2,4}$cm.
Cho hình thoi \(ABCD\), hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Biết \(AC = 6\)cm; \(BD = 8\)cm. Tính độ dài cạnh của hình thoi \(ABCD\)
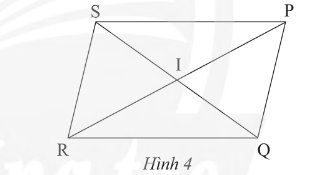
Cho hình bình hành \(PQRS\) với \(I\) là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.
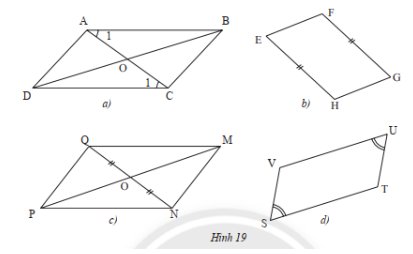
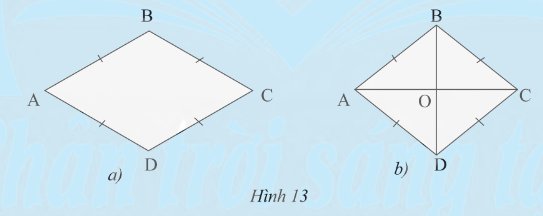
a) Hình thoi có là hình bình hành không?
b) Cho hình thoi \(ABCD\) có \(O\) là giao điểm của hai đường chéo (Hình 13b). Các tam giác \(OAB\), \(OCB\), \(OCD\), \(OAD\) có bằng nhau không?
Cho hình bình hành \(ABCD\). Gọi \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\)
a) Chứng minh rằng tứ giác \(EBFD\) là hình bình hành
b) Gọi \(O\) là giao điểm của hai đường chéo của hình bình hành \(ABCD\). Chứng minh rằng ba điểm \(E\), \(O\), \(F\) thẳng hàng.
Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4cm và 5cm. Tìm độ dài hai cạnh còn lại.
Cho tứ giác \(ABCD\) có các cạnh đối song song. Gọi \(O\) là giao điểm của hai đường chéo. Hãy chứng tỏ:
- Tam giác \(ABC\) bằng tam giác \(CDA\)
- Tam giác \(OAB\) bằng tam giác \(OCD\)