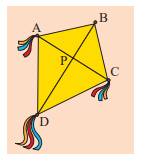
Tia DB là tia phân giác của góc \(\widehat {ADC}\)
Bài 2. Tia phân giác
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
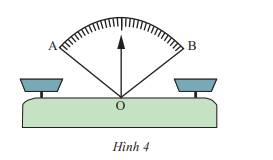
Em hãy cho biết khi cân thăng bằng thì kim ở vị trí nào của \(\widehat {AOB}\)(Hình 4)
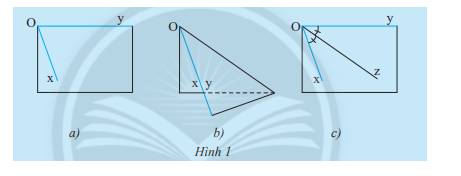
Vẽ \(\widehat {xOy}\) lên một tờ giấy như trong hình 1a. Gấp giấy sao cho cạnh Oy trùng với cạnh Ox. Nếp gấp cho ta vị trí của tia Oz. Theo em, tia Oz đã chia\(\widehat {xOy}\) thành hai góc như thế nào?
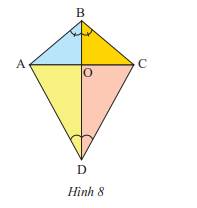
a) Trong Hình 8, tìm tia phân giác của góc \(\widehat {ABC},\widehat {ADC}\)
b) Cho biết \(\widehat {ABC} = 100^\circ ;\widehat {ADC} = 60^\circ \). Tính số đo của các góc \(\widehat {ABO},\widehat {ADO}\)
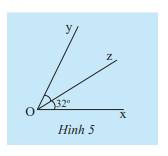
Trong Hình 5, nếu tia Oz là tia phân giác của \(\widehat {xOy}\) thì số đo của \(\widehat {xOy}\) bằng bao nhiêu?
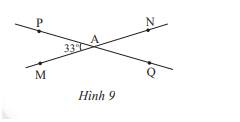
Cho đường thẳng MN, PQ cắt nhau tại A và tạọ thành widehat {PAM} 33^circ (Hình 9)a) Tính số đo các góc còn lại.b) Vẽ tia At là tia phân giác của widehat {PAN}. Hãy tính số đo của widehat {tAQ}. Vẽ At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của widehat {MAQ}
Đọc tiếp
Cho đường thẳng MN, PQ cắt nhau tại A và tạọ thành \(\widehat {PAM} = 33^\circ \) (Hình 9)
a) Tính số đo các góc còn lại.
b) Vẽ tia At là tia phân giác của \(\widehat {PAN}\). Hãy tính số đo của \(\widehat {tAQ}\). Vẽ At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của \(\widehat {MAQ}\)
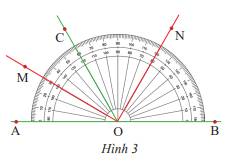
Tìm tia phân giác của các góc: \(\widehat {AOC}\) và \(\widehat {COB}\) trong hình 3.
Vẽ góc bẹt \(\widehat {xOy}\). Vẽ tia phân giác Oz của góc đó. Vẽ tia phân giác Ot của \(\widehat {xOz}\). Vẽ tia phân giác Ov của \(\widehat {zOy}\) . Tính \(\widehat {tOv}\).
Vẽ hai góc kề bù \(\widehat {xOy},\widehat {yOx'}\), biết \(\widehat {xOy} = 120^\circ \). Gọi Oz là tia phân giác của \(\widehat {xOy}\), Oz’ là tia phân giác của \(\widehat {yOx'}\). Tính \(\widehat {zOy},\widehat {yOz'},\widehat {zOz'}\).
Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho \(\widehat {xOz} = 135^\circ \). Vẽ tia Ot sao cho \(\widehat {yOt} = 90^\circ \) và \(\widehat {zOt} = 135^\circ \). Gọi Ov là tia phân giác của \(\widehat {xOt}\). Các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) có phải là hai góc đối đỉnh không? Vì sao?