Bài 1: Cho hình bình hành ABCD. Trên BD lấy điểm E, gọi F là điểm đối xứng với C qua E. Qua F, kẻ Fx song song với AD, Fy song song với AB; Fx cắt AB tại I, Fy cắt AD tại K. Chứng minh rằng: I, K, E thẳng hàng
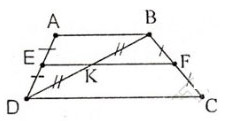
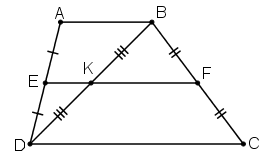
Bài 2: Cho hình thang ABCD có đáy lớn CD. Qua A kẻ đường thẳng AK song song với BC. Qua B kẻ đường thảng BI song song với AB. BI cắt AC ở F, AK cắt BD ở E. Chứng minh rằng:
a) EF // AB;
b) AB^2 CD. EF
Bài 3: Cho hình bình hành ABCD, điểm E thuộc cạnh AB, điểm F thuộc cạnh AD. Đư...
Đọc tiếp
Bài 1: Cho hình bình hành ABCD. Trên BD lấy điểm E, gọi F là điểm đối xứng với C qua E. Qua F, kẻ Fx song song với AD, Fy song song với AB; Fx cắt AB tại I, Fy cắt AD tại K. Chứng minh rằng: I, K, E thẳng hàng
Bài 2: Cho hình thang ABCD có đáy lớn CD. Qua A kẻ đường thẳng AK song song với BC. Qua B kẻ đường thảng BI song song với AB. BI cắt AC ở F, AK cắt BD ở E. Chứng minh rằng:
a) EF // AB;
b) AB^2 = CD. EF
Bài 3: Cho hình bình hành ABCD, điểm E thuộc cạnh AB, điểm F thuộc cạnh AD. Đường thẳng qua D và song song với EF cắt AC ở I. Đường thẳng qua B và song song với EF cắt AC ở K. Chứng minh rằng:
a) AI = CK
b) AB/AE + AD/AF = AC/AN ( N là giao điểm của EF và AC)
Bài 4: Cho hình bình hành AABCD. Đường thẳng đi qua D cắt AC, AB, CB theo thứ tự ở M, N, K. Chứng minh rằng:
a) DM2 = MN.MK
b) DM/DN + DM/DK = 1
Bài 5: Cho hình thoi ABCD. Qua C kẻ đường thẳng d cắt các tia đối của các tia BA, CA theo thứ tự ở E và F. Chứng minh rằng:
a) EM/AB = AD/DF
b) EBD đồng dạng với BDF;
c) Góc BID bằng 120 độ ( I là giao điểm của DE và BF)
Bài 6: Cho cân tại A có BC = 2a. M là trung điểm của BC. Lấy các điểm D, E theo thứ tự thuộc các cạnh AB, AC sao cho
CMR: Tích BD.CE không đổi
CMR: DM là phân giác của góc
Tính chu vi của AED nếu ABC đều
Bài 7: Cho ( AB khác AC) Gọi E và F theo thứ tự là các hình chiếu của B và C trên tia phân giác của góc A. Gọi K là giao điểm của các đường thẳng FB và CE. Chứng minh rằng: AK là tia phân giác của góc ngoài tại đỉnh A của
Bài 8: Cho hình thang ABCD( AB //CD). M là trung điểm của cạnh CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM và AC
a) Chứng minh rằng: IK//AB
b) Đường thẳng IK cắt AD và BC theo thứ tự ở E và F. Chứng minh IE = IK = KF