\(a,x=16\Leftrightarrow A=\dfrac{-3\cdot4+1}{4-3}=\dfrac{-11}{1}=-11\\ b,B=\dfrac{3\sqrt{x}-2-\sqrt{x}+3-\left(3\sqrt{x}-2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{2\sqrt{x}+1-3x+8\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{-3x+10\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{\left(\sqrt{x}-3\right)\left(-3\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{-3\sqrt{x}+1}{\sqrt{x}-2}\)
\(c,B>-3\Leftrightarrow B+3>0\Leftrightarrow\dfrac{-3\sqrt{x}+1+3\sqrt{x}+6}{\sqrt{x}-2}>0\\ \Leftrightarrow\dfrac{7}{\sqrt{x}-2}>0\Leftrightarrow\sqrt{x}-2>0\left(7>0\right)\\ \Leftrightarrow x>4\)
\(d,P=\dfrac{A}{B}=\dfrac{-3\sqrt{x}+1}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-2}{-3\sqrt{x}+1}\\ P=\dfrac{\sqrt{x}-2}{\sqrt{x}-3}=1+\dfrac{1}{\sqrt{x}-3}>1\left(\dfrac{1}{\sqrt{x}-3}>0\right)\)
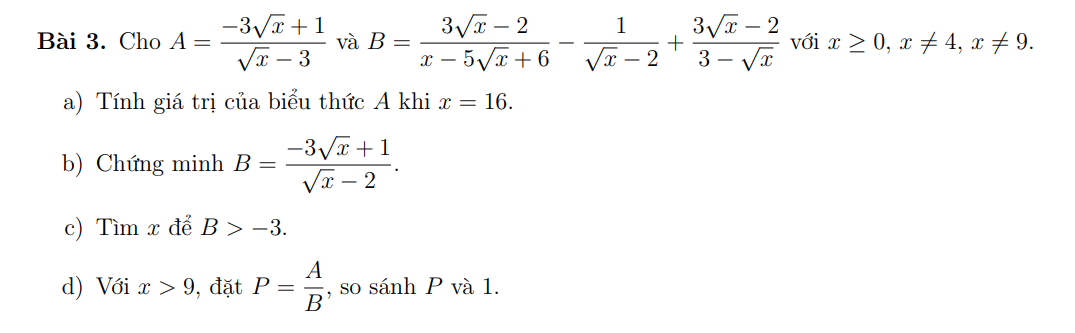 help me !!!
help me !!!




