Question

Hai gương phẳng G1 và G2 đặt vuông góc với nhau, mặt phản xạ quay vào nhau. Tia tới SI được chiếu lên gương G1 lần lượt phản xạ trên gương G1 rồi trên gương G2.

a, Nêu cách vẽ đường đi của tia sáng

b,Góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương G2 có giá trị là bao nhiêu?

Answer 1

a, Đầu tiên vẽ tia tới chiếu đến gương G1 tại I, rồi phản đến gương G2 tại điểm I' , rồi phản xạ tiếp qua điểm R

b, Ta có tia pháp tuyến \(NI\perp I\) (G1) , \(NI'\perp I'\left(G2\right)\)

mà 2 gương  G1 , G2 vuông góc vói nhau 

\(\Rightarrow\left\{{}\begin{matrix}i=90^o-45^o=45^o\\i=i'\Leftrightarrow i'=45^o\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}i2=90^o-45^o=45^o\\i2=i2'\Leftrightarrow i2'=45^o\end{matrix}\right.\)

Góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương G2 : \(45^o+45^o+45^o+45^o=180^o\)

Answer 2

Tham khảo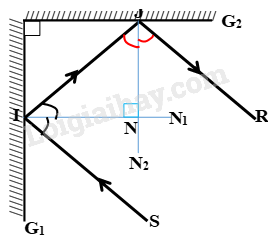

Do hai gương đặt vuông góc với nhau nên hai pháp tuyến IN1IN1 và JN2JN2 cũng vuông góc với nhau.

Định luật phản xạ tại gương G1G1:

ˆSIN=ˆNIJ⇒ˆSIJ=2ˆNIJ(1)SIN^=NIJ^⇒SIJ^=2NIJ^(1)

Định luật phản xạ tại gương G2G2:

ˆIJN=ˆNJR⇒ˆIJR=2ˆIJN(2)IJN^=NJR^⇒IJR^=2IJN^(2)

ΔIJNΔIJN vuông tại :

ˆNIJ+ˆNJI=900NIJ^+NJI^=900

⇒ˆSIJ+ˆIJR=2ˆNIJ+2ˆNJI=2(ˆNIJ+ˆNJI)=1800⇒SIJ^+IJR^=2NIJ^+2NJI^=2(NIJ^+NJI^)=1800

Vậy tia tới  song song với tia phản xạ . Góc tạo bởi tia tới   và tia phản xạ cuối cùng trên gương G2G2 có giá trị 1800