CÓ TRÊN MẠNG NHÉ;)
Ta có:
\(\dfrac{1}{1+a}=1-\dfrac{1}{1+b}+1-\dfrac{1}{1+c}\)
=\(\dfrac{b}{1+b}+\dfrac{c}{1+c}\) lớn hơn hoặc bằng \(2\sqrt{\dfrac{bc}{\left(1+b\right)\left(1+c\right)}}\)
Tương tự:
\(\dfrac{1}{1+b}\) lớn hơn hoặc bằng \(2\sqrt{\dfrac{ac}{\left(1+a\right)\left(1+c\right)};}\) \(\dfrac{1}{1+c}\) lớn hơn hoặc bằng \(2\sqrt{\dfrac{ab}{\left(1+a\right)\left(1+b\right)}}\)
\(\dfrac{1}{\left(1+a\right)\left(1+b\right)\left(1+c\right)}\) lớn hơn hoặc bằng \(8\sqrt{\dfrac{a^2b^2c^2}{\left(1+a\right)\left(1+b\right)\left(1+c\right)}}\)
\(\dfrac{1}{\left(1+a\right)\left(1+b\right)\left(1+c\right)}\) lớn hơn hoặc bằng \(\dfrac{8abc}{\left(1+a\right)\left(1+b\right)\left(1+c\right)}\)
=> abc bé hơn hoặc bằng \(\dfrac{1}{8}\)
Dấu "=" xảy ra <=> a=b=c và \(\dfrac{1}{1+a}=\dfrac{1}{1+b}=\dfrac{1}{1+c}=2< =>a=b=c=\dfrac{1}{2}\)
Vậy MAXQ là \(\dfrac{1}{8}\) khi a=b=c=\(\dfrac{1}{2}\)



 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)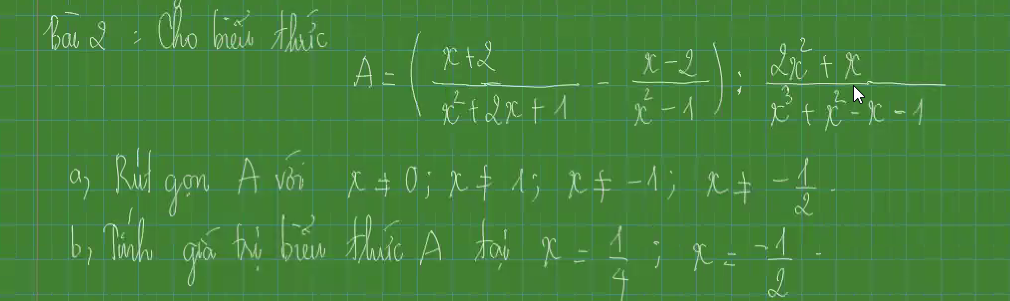
 Giúp em vs ạ
Giúp em vs ạ