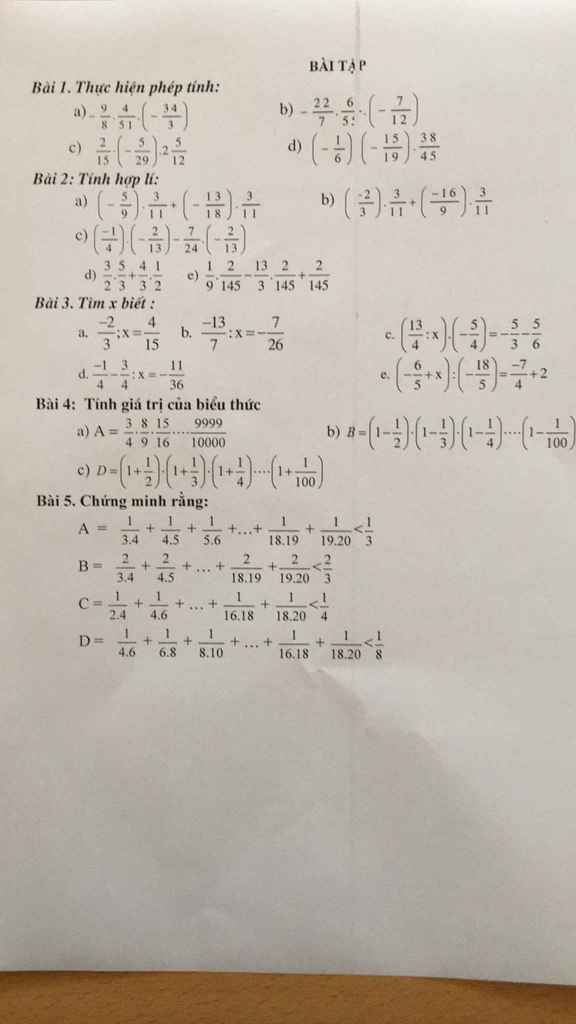\(A=\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{19.20}=\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{20}=\dfrac{1}{3}-\dfrac{1}{20}< \dfrac{1}{3}\)
\(B=\dfrac{2}{3.4}+\dfrac{2}{4.5}+...+\dfrac{2}{19.20}=2\left(\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{19.20}\right)=2\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)=2\left(\dfrac{1}{3}-\dfrac{1}{20}\right)=\dfrac{2}{3}-\dfrac{2}{20}< \dfrac{2}{3}\)
\(C=\dfrac{1}{2.4}+\dfrac{1}{4.6}+...+\dfrac{1}{18.20}=\dfrac{1}{2}\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{18.20}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{18}-\dfrac{1}{20}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{20}\right)=\dfrac{1}{4}-\dfrac{1}{40}< \dfrac{1}{4}\)
\(D=\dfrac{1}{4.6}+\dfrac{1}{6.8}+...+\dfrac{1}{18.20}=\dfrac{1}{2}\left(\dfrac{2}{4.6}+\dfrac{2}{6.8}+...+\dfrac{2}{18.20}\right)=\dfrac{1}{2}\left(\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+...+\dfrac{1}{18}-\dfrac{1}{20}\right)=\dfrac{1}{2}\left(\dfrac{1}{4}-\dfrac{1}{20}\right)=\dfrac{1}{8}-\dfrac{1}{40}< \dfrac{1}{8}\)
mn giúp em vs ạ, em đang gấp