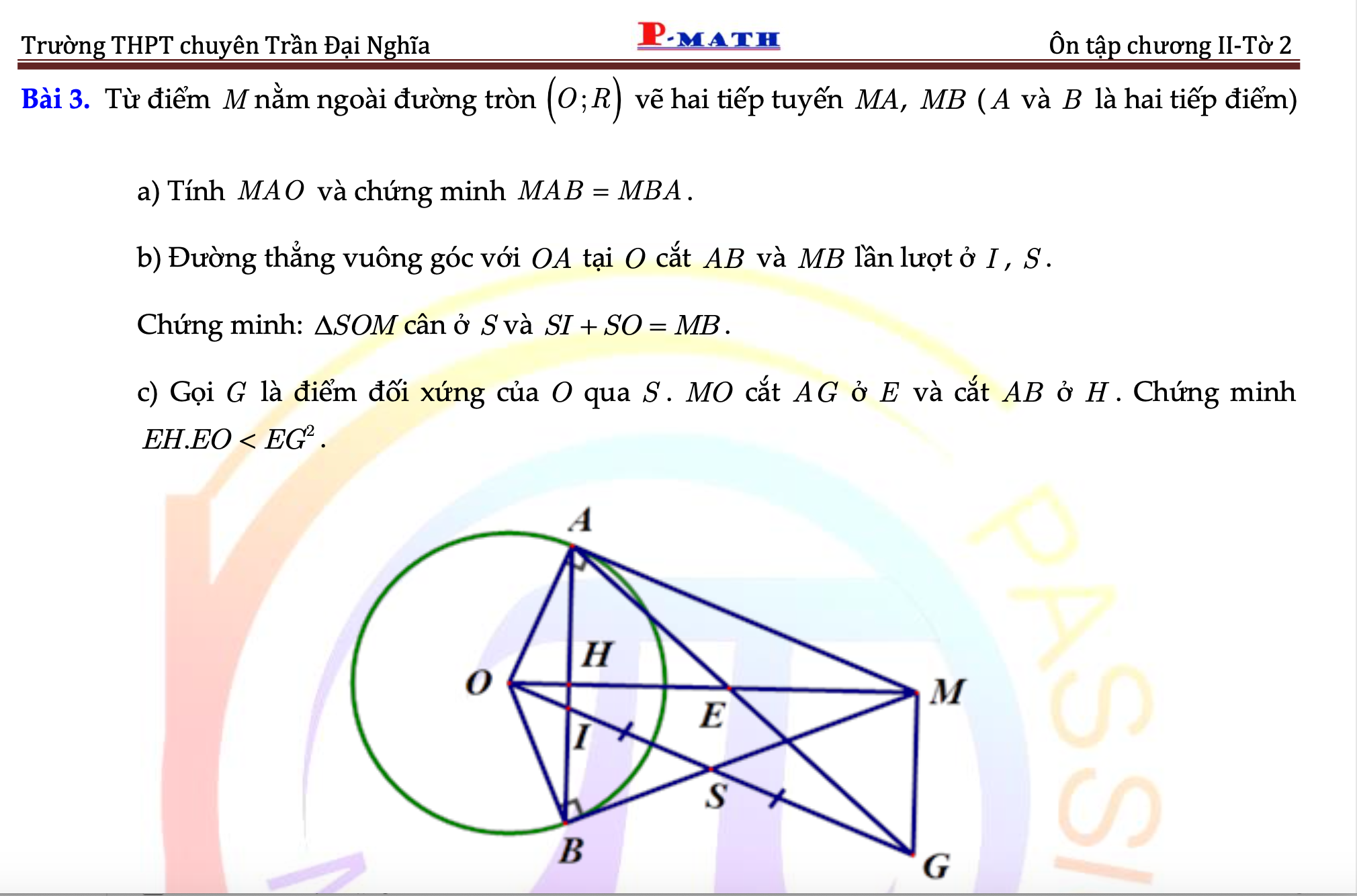
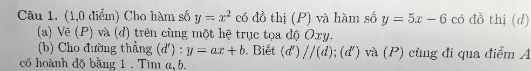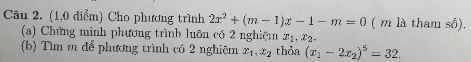Lời giải:
1.
Vì $AC$ là tiếp tuyến của $(O)$ nên $OC\perp AC$
$\Rightarrow \widehat{OCA}=90^0$
Tương tự: $\widehat{OMA}=90^0$
Tứ giác $ACOM$ có tổng 2 góc đối $\widehat{OCA}+\widehat{OMA}=180^0$ nên là tứ giác nội tiếp.
2.
$ON\perp BN$ (theo tính chất tiếp tuyến) nên $ONB$ là tam giác vuông tại $N$
Áp dụng định lý Pitago cho tam giác này:
$BN=\sqrt{OB^2-ON^2}=\sqrt{(2R)^2-R^2}=\sqrt{3}R$
Tương tự phần a, ta cm được $ONBC$ là tgnt.
$OB$ cắt $(O)$ tại $T$
$TB=OB-OT=2R-R=R$ nên $OT=TB$ hay $T$ là trung điểm của $OB$
Tam giác $ONB$ vuông tại $N$ nên trung tuyến $NT=\frac{OB}{2}=OT=ON$ nên tam giác $ONT$ là tam giác đều.
Tương tự: $OCT$ là tam giác đều
$\widehat{NBC}=180^0-\widehat{NOC}=180^0-(\widehat{NOT}+\widehat{COT})=180^0-(60^0+60^0)=60^0$
3.
Vì $AM\parallel BN$ (cùng vuông góc với $MN$) nên theo định lý Talet:
$\frac{AI}{IN}=\frac{AM}{BN}$
Mà: $BN=BC, AM=AC$ theo tính chất tiếp tuyến giao nhau
$\Rightarrow \frac{AI}{IN}=\frac{AC}{BC}(*)$
Theo định lý Talet đảo thì $IC\parallel BN$. Mà $BN\perp MN$ nên IC\perp MN$
----------------
Dễ thấy $E, F$ lần lượt là trung điểm của $MC, NC$ theo tính chất 2 tiếp tuyến cắt nhau
Do đó: $EF\parallel MN$ (tính chất đường trung bình)
Cũng theo tính chất 2 tiếp tuyến cắt nhau thì thấy:
$OA$ là phân giác $\widehat{COM}$; $OB$ là phân giác $\widehat{CON}$
$\widehat{COM}+\widehat{CON}=180^0$
$\Rightarrow OA\perp OB$
Mà $EC\perp AO$ nên $EC\parallel OB$
Áp dụng định lý Talet:
$\frac{AC}{CB}=\frac{AE}{EO}(**)$
Từ $(*); (**)\Rightarrow \frac{AI}{IN}=\frac{AE}{EO}$
Theo định lý Talet đảo thì $EI\parallel ON$ hay $EI\parallel MN$
Do vậy:
$EI\parallel EF$ (cùng song song với $MN$)
$\Rightarrow E,I,F$ thẳng hàng.
1.
Vì ACAC là tiếp tuyến của (O)(O) nên OC⊥ACOC⊥AC
⇒ˆOCA=900⇒OCA^=900
Tương tự: ˆOMA=900OMA^=900
Tứ giác ACOMACOM có tổng 2 góc đối ˆOCA+ˆOMA=1800OCA^+OMA^=1800 nên là tứ giác nội tiếp.
2.
ON⊥BNON⊥BN (theo tính chất tiếp tuyến) nên ONBONB là tam giác vuông tại NN
Áp dụng định lý Pitago cho tam giác này:
BN=√OB2−ON2=√(2R)2−R2=√3RBN=OB2−ON2=(2R)2−R2=3R
Tương tự phần a, ta cm được ONBCONBC là tgnt.
OBOB cắt (O)(O) tại TT
TB=OB−OT=2R−R=RTB=OB−OT=2R−R=R nên OT=TBOT=TB hay TT là trung điểm của OBOB
Tam giác ONBONB vuông tại NN nên trung tuyến NT=OB2=OT=ONNT=OB2=OT=ON nên tam giác ONTONT là tam giác đều.
Tương tự: OCTOCT là tam giác đều
ˆNBC=1800−ˆNOC=1800−(ˆNOT+ˆCOT)=1800−(600+600)=600NBC^=1800−NOC^=1800−(NOT^+COT^)=1800−(600+600)=600
3.
Vì AM∥BNAM∥BN (cùng vuông góc với MNMN) nên theo định lý Talet:
AIIN=AMBNAIIN=AMBN
Mà: BN=BC,AM=ACBN=BC,AM=AC theo tính chất tiếp tuyến giao nhau
⇒AIIN=ACBC(∗)⇒AIIN=ACBC(∗)
Theo định lý Talet đảo thì IC∥BNIC∥BN. Mà BN⊥MNBN⊥MN nên IC\perp MN$
----------------
Dễ thấy E,FE,F lần lượt là trung điểm của MC,NCMC,NC theo tính chất 2 tiếp tuyến cắt nhau
Do đó: EF∥MNEF∥MN (tính chất đường trung bình)
Cũng theo tính chất 2 tiếp tuyến cắt nhau thì thấy:
OAOA là phân giác ˆCOMCOM^; OBOB là phân giác ˆCONCON^
ˆCOM+ˆCON=1800COM^+CON^=1800
⇒OA⊥OB⇒OA⊥OB
Mà EC⊥AOEC⊥AO nên EC∥OBEC∥OB
Áp dụng định lý Talet:
ACCB=AEEO(∗∗)ACCB=AEEO(∗∗)
Từ (∗);(∗∗)⇒AIIN=AEEO(∗);(∗∗)⇒AIIN=AEEO
Theo định lý Talet đảo thì EI∥ONEI∥ON hay EI∥MNEI∥MN
Do vậy:
EI∥EFEI∥EF (cùng song song với MNMN)
⇒E,I,F⇒E,I,F thẳng hàng.



 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 


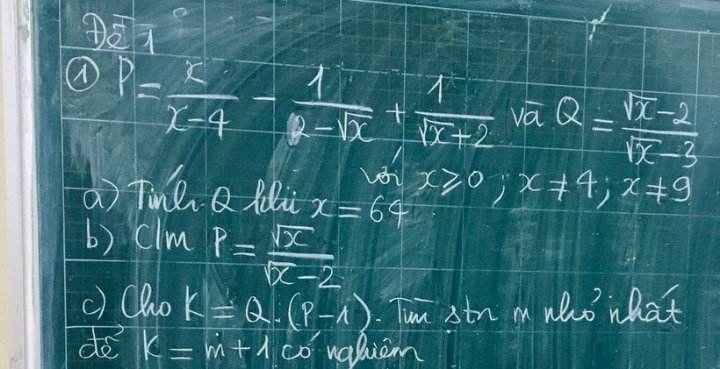 giúp mình câu c với ạ, mình cảm ơn nhiều
giúp mình câu c với ạ, mình cảm ơn nhiều