2 bài hơi nhiều đó bạn mình tách ra làm nha :))
70)
a) ΔABC cân tại A ⇒ ∠ABC = ∠ACB
⇒∠ABM = ∠ACN (vì ∠ABC + ∠ABM = ∠ACB + ∠ACN = 1800)
Xét ΔABM và ΔACN có:
AB = AC (gt); ∠ABM = ∠ACN (cmtrên); MB = NC (gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (Cạnh tương ứng)
⇒ ΔAMN cân tại A
b) Xét ΔHBM và ΔKCN có:
∠H = ∠K (=900)
MB = NC (gt)
∠HMB = ∠KNC (ΔAMN cân ở A)
⇒ ΔHBM = ΔKCN (Cạnh huyền – góc nhọn)
⇒ HB =KC (Cạnh tương ứng)
c) Ta có AM = AN (1) (ΔAMN cân ở A)
HM = KN (2) (ΔHBM = ΔKCN)
Từ (1) và (2) suy ra AM – HM = AN -KN hay AH = AK
d) Ta có ∠B2 = ∠C2 (ΔHBM = ΔKCN)
∠B3 = ∠B2 (Đối đỉnh)
∠C3 = ∠C2 (Đối đỉnh)
⇒ ∠B3 = ∠C3 ⇒ ΔBOC cân ở O
e)
+) ΔABC cân có ∠BAC = 600 ⇒ ΔABC đều ⇒ ∠B1 =600
Có ΔABM cân (Vì AB = BM = BC)
⇒ ∠M = ∠B1/2= 600/2 =300 (T/c góc ngoài tam giác)
⇒ ∠N = 300 (ΔAMN cận tại A)
⇒ ∠MAN = 1800 – (300 +300) = 1200
+) Xét ΔBHM có ∠H = 900, ∠M = 300 ⇒ ∠B2 =900 – ∠M = 900 – 300 =600
⇒ ∠B3 =600 (Do ∠B2 và ∠B3 đối đỉnh)
Mà ΔBOC là Δcân nên Δ BOC là Δđều.
69)
∆ABD và ∆ACD có:
AB = AC (gt)
DB = DC (gt)
AD cạnh chung.
Nên ∆ABD = ∆ACD (c.c.c)
\(\Rightarrow\) \(\widehat{A_1}=\widehat{A_2}\left(1\right)\)
Gọi H là giao điểm của AD và a.
∆AHB và ∆AHC có:
AB = AC (gt)
\(\widehat{A_1}=\widehat{A_2}\left(1\right)\)
AH cạnh chung.
Nên ∆AHB = ∆AHC (c.g.c)
Suy ra: \(\widehat{H_1}=\widehat{H_2}\)
Ta lại có: \(\widehat{H_1}+\widehat{H_2}=180^o\Rightarrow\widehat{H_1}=\widehat{H_2}=90^o\)
Vậy AD ⊥ a.



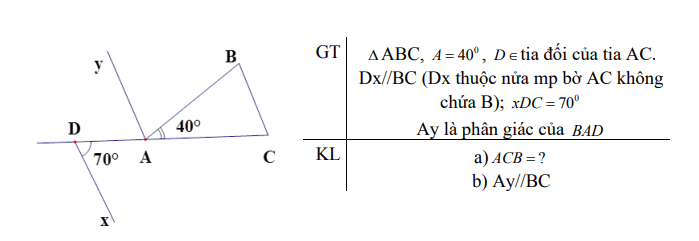
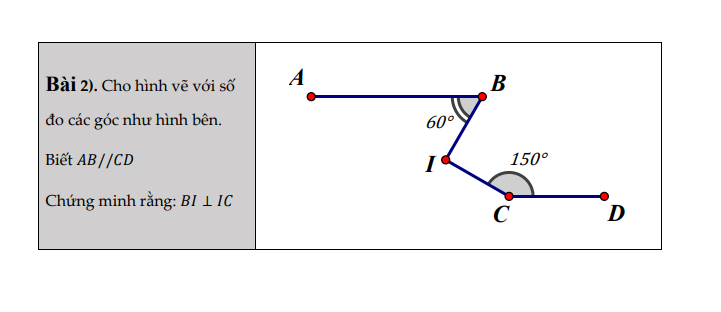
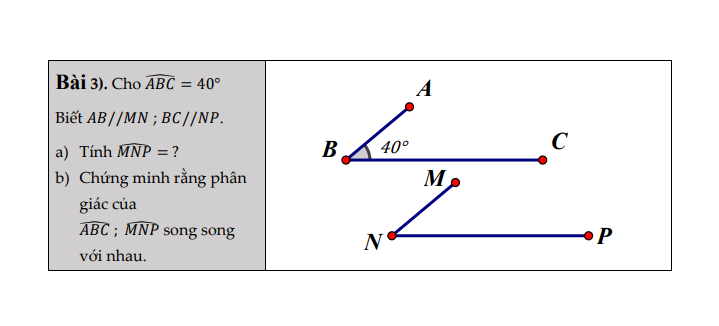

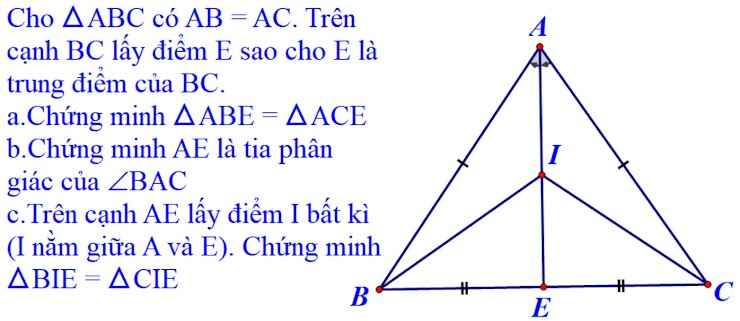
 các bạn giải hộ mik nha,cảm ơn ơn các bạn nhiều !!!
các bạn giải hộ mik nha,cảm ơn ơn các bạn nhiều !!!
