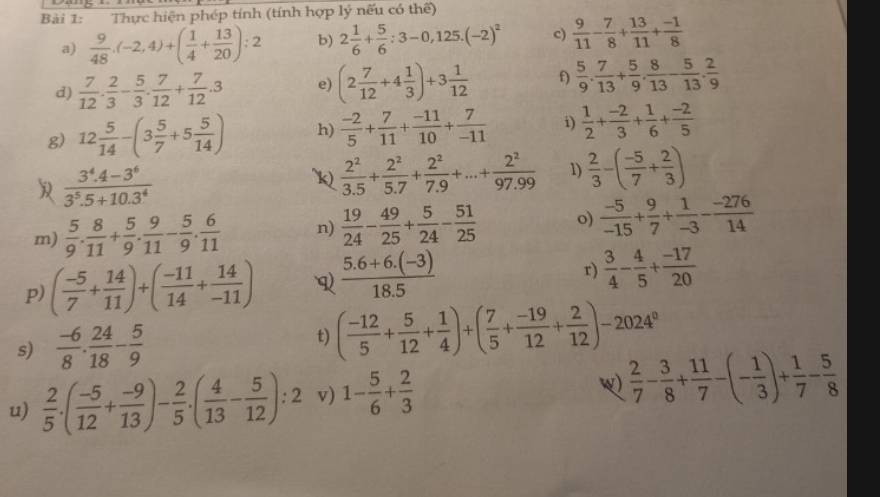j: \(\dfrac{3^4\cdot4-3^6}{3^5\cdot5+10\cdot3^4}\)
\(=\dfrac{3^4\cdot4-3^4\cdot9}{3^4\cdot15+3^4\cdot10}\)
\(=\dfrac{3^4\left(4-9\right)}{3^4\left(15+10\right)}=\dfrac{-5}{25}=\dfrac{-1}{5}\)
k: \(\dfrac{2^2}{3\cdot5}+\dfrac{2^2}{5\cdot7}+\dfrac{2^2}{7\cdot9}+...+\dfrac{2^2}{97\cdot99}\)
\(=2\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}\right)\)
\(=2\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\right)\)
\(=2\left(\dfrac{1}{3}-\dfrac{1}{99}\right)=2\cdot\dfrac{32}{99}=\dfrac{64}{99}\)
q: \(\dfrac{5\cdot6+6\cdot\left(-3\right)}{18\cdot5}=\dfrac{6\left(5-3\right)}{6\cdot3\cdot5}=\dfrac{2}{15}\)
w: \(\dfrac{2}{7}-\dfrac{3}{8}+\dfrac{11}{7}-\left(-\dfrac{1}{3}\right)+\dfrac{1}{7}-\dfrac{5}{8}\)
\(=\left(\dfrac{2}{7}+\dfrac{11}{7}+\dfrac{1}{7}\right)+\left(-\dfrac{3}{8}-\dfrac{5}{8}\right)+\dfrac{1}{3}\)
\(=2-1+\dfrac{1}{3}=1+\dfrac{1}{3}=\dfrac{4}{3}\)