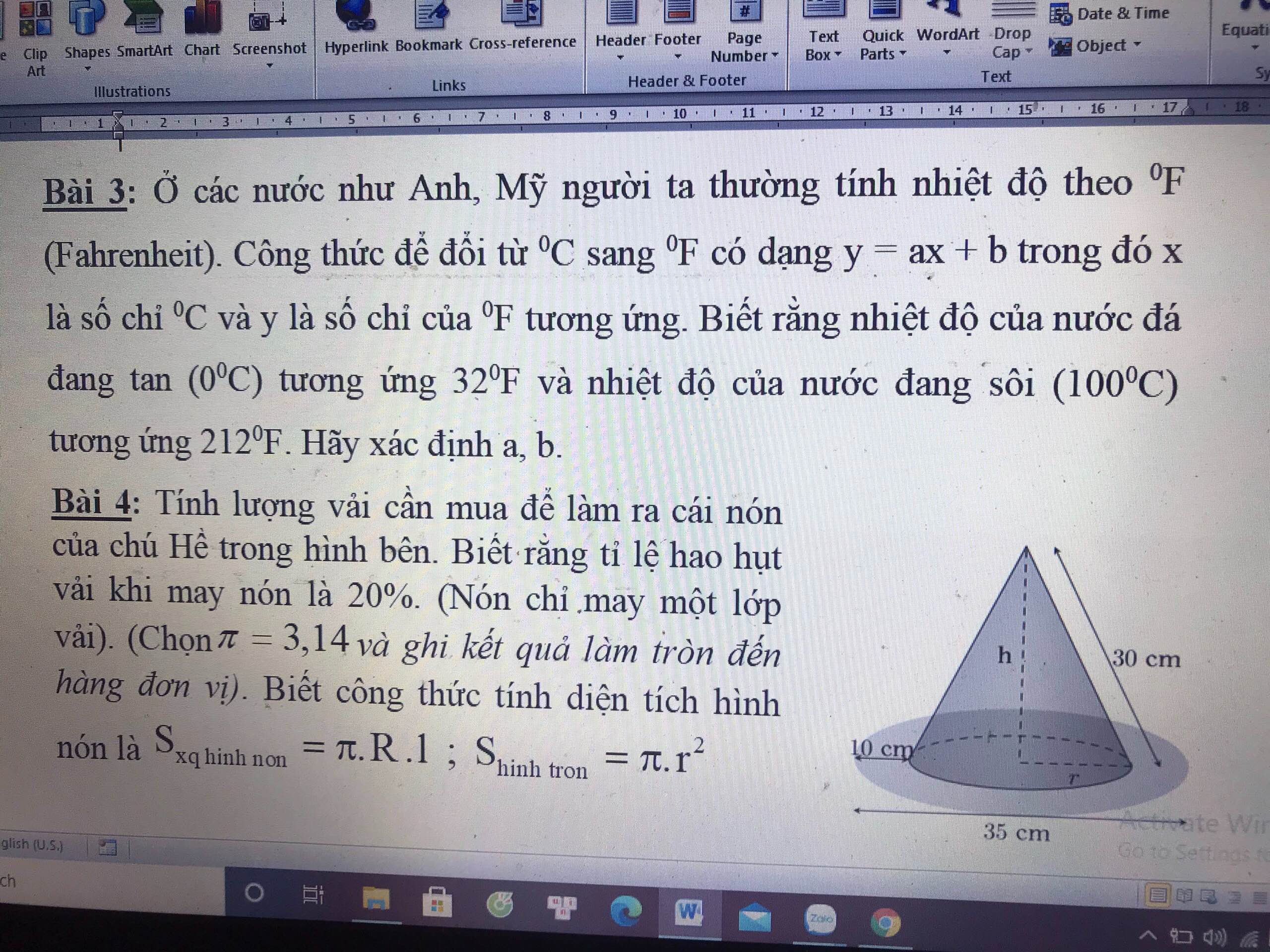
a) Ta có: \(\angle BFC=\angle BEC=90\Rightarrow BCEF\) nội tiếp
Ta có: \(\angle HEC+\angle HDC=90+90=180\Rightarrow EHDC\) nội tiếp
b) BCEF nội tiếp \(\Rightarrow\angle KBF=\angle KEC\)
Xét \(\Delta KBF\) và \(\Delta KEC:\) Ta có: \(\left\{{}\begin{matrix}\angle KBF=\angle KEC\\\angle EKCchung\end{matrix}\right.\)
\(\Rightarrow\Delta KBF\sim\Delta KEC\left(g-g\right)\Rightarrow\dfrac{KB}{KE}=\dfrac{KF}{KC}\Rightarrow KB.KC=KE.KF\)
Tương tự \(\Rightarrow\Delta KBI\sim\Delta KAC\left(g-g\right)\Rightarrow\dfrac{KB}{KA}=\dfrac{KI}{KC}\Rightarrow KI.KA=KB.KC\)
\(\Rightarrow KI.KA=KE.KF\)
c) Vì \(MN\parallel AC\) mà \(AC\bot BH\Rightarrow MN\bot BH\)
Vì \(MN\parallel AC\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{BM}{AC}=\dfrac{KB}{KC}\\\dfrac{BN}{AC}=\dfrac{BD}{DC}\end{matrix}\right.\left(4\right)\)
Ta có: \(\angle FEB=\angle FCB\left(BCEFnt\right)=\angle BED\left(EHDCnt\right)\)
\(\Rightarrow EB\) là phân giác trong \(\angle KED\Rightarrow\dfrac{KB}{BD}=\dfrac{EK}{ED}\left(1\right)\)
Ta có: EB là phân giác trong \(\angle KED\) mà \(EB\bot EC\)
\(\Rightarrow EC\) là phân giác ngoài \(\angle KED\) \(\Rightarrow\dfrac{EK}{ED}=\dfrac{CK}{CD}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{KB}{BD}=\dfrac{KC}{CD}\Rightarrow\dfrac{KB}{KC}=\dfrac{BD}{CD}\left(4\right)\)
Từ (3) và (4) \(\Rightarrow\dfrac{BM}{AC}=\dfrac{BN}{AC}\Rightarrow BM=BN\)
\(\Rightarrow\) HB là trung tuyến của \(\Delta HMN\) mà \(HB\bot MN\Rightarrow\Delta MHN\) cân tại H
\(\Rightarrow HM=HN\)