\(a,ĐK:x\le3\\ PT\Leftrightarrow x^2+x+1=x^2-6x+9\\ \Leftrightarrow7x=8\Leftrightarrow x=\dfrac{8}{7}\left(tm\right)\\ b,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow x^2-6x+6=4x^2-4x+1\\ \Leftrightarrow3x^2+2x-5=0\\ \Leftrightarrow\left(x-1\right)\left(3x+5\right)=0\Leftrightarrow x=1\left(x\ge\dfrac{1}{2}\right)\\ c,ĐK:x\ge1\\ PT\Leftrightarrow27x-18=x^2-2x+1\\ \Leftrightarrow x^2-29x+19=0\\ \Delta=29^2-4\cdot19=765\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{29+3\sqrt{85}}{2}\left(n\right)\\x=\dfrac{29-3\sqrt{85}}{2}\left(l\right)\end{matrix}\right.\)
\(d,\Leftrightarrow\sqrt{x^2+3x-3}=3-2x\left(x\le\dfrac{3}{2}\right)\\ \Leftrightarrow x^2+3x-3=4x^2-12x+9\\ \Leftrightarrow3x^2-15x+12=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\left(l\right)\\x=1\left(n\right)\end{matrix}\right.\\ e,ĐK:x\ge3\\ PT\Leftrightarrow x^2-3x-2=x-3\\ \Leftrightarrow x^2-4x+1=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2+\sqrt{3}\left(n\right)\\x=2-\sqrt{3}\left(l\right)\end{matrix}\right.\)
\(f,ĐK:x\ge1\\ PT\Leftrightarrow9x-9=x^2+8x-11\\ \Leftrightarrow x^2-x-2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\left(n\right)\\x=2\left(n\right)\end{matrix}\right.\)





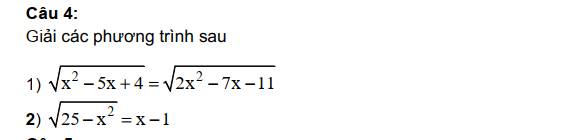



 Giúp em vs ạ
Giúp em vs ạ giúp em với ạ
giúp em với ạ
