9. \(K=2\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{a^2-a}\right)=2\left(\dfrac{1-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\dfrac{\sqrt{a}+1}{a\left(a-1\right)}=2\left(\dfrac{2-\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\dfrac{\sqrt{a}+1}{a\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{4-2\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}.a\left(\sqrt{a}-1\right)=\dfrac{4a-2a\sqrt{a}}{\sqrt{a}}=\dfrac{\sqrt{a}\left(4\sqrt{a}-2a\right)}{\sqrt{a}}=4\sqrt{a}-2a\)
Chương I - Căn bậc hai. Căn bậc ba
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Giải giúp em câu b với c ạ. E cần gấp 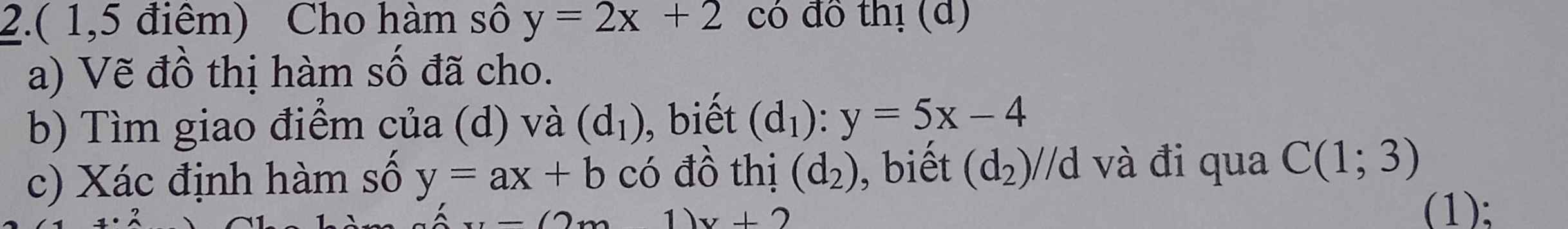
Giúp e vs ạ...e cần gấp 😥 cảm ơn rất nhiều ạ!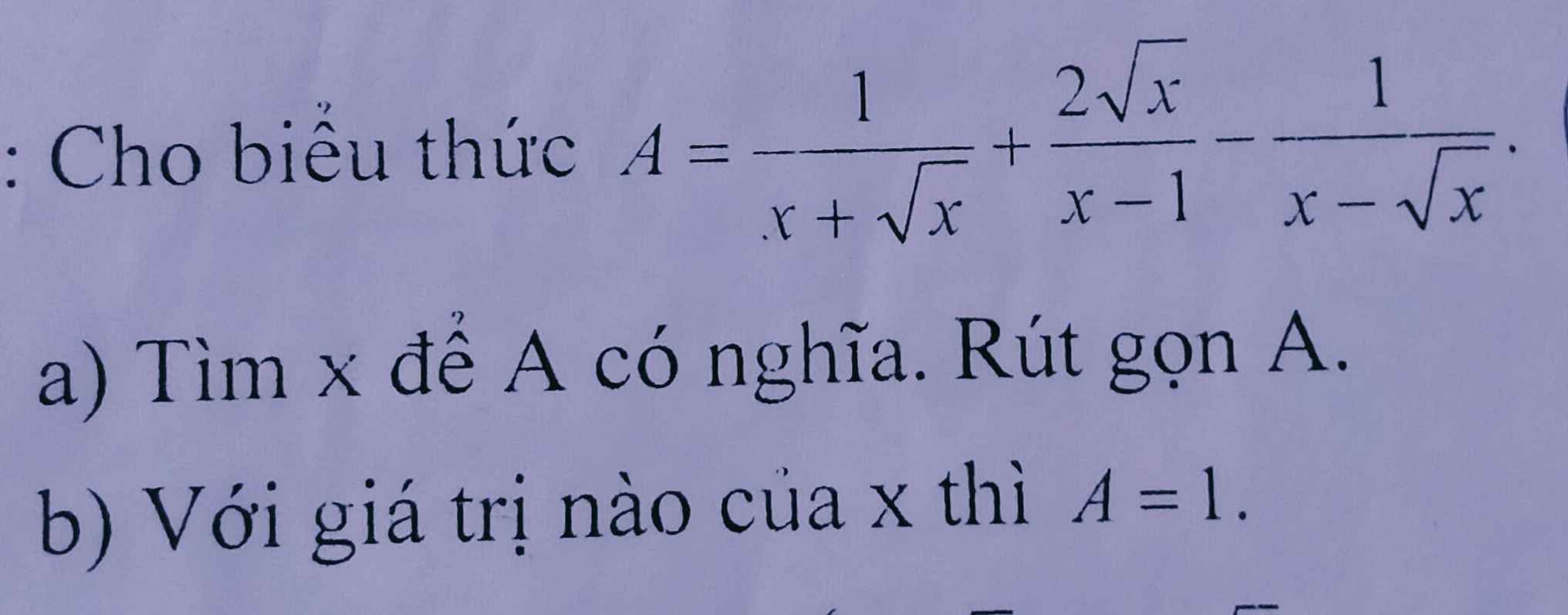
giúp em câu e bài giải pt

giúp e bài 1 với ạ,e cảm ơn

Giúp e 2 bài này với ;-;
Giúp e bài 4 với ạ
Giải hộ mình bài này với mình đang cần gấp 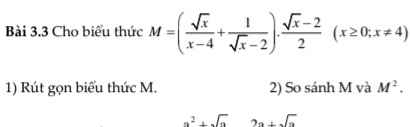
anh e giúp mik mấy câu này vs! sau đợt nghỉ dịch này chắc não ko còn j. NHANH NHÁ, MIK ĐAG CẦN GẤP!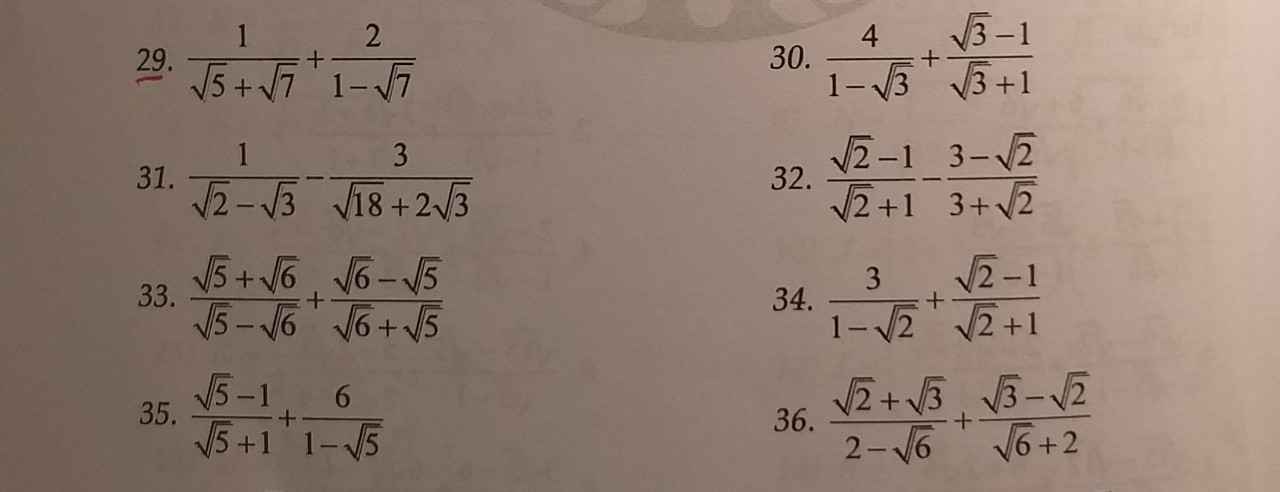
giúp em bài 4 với ạ em cần gấp 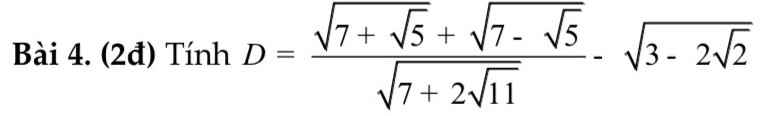
 Giải giúp e bài 9,10,11 với aạ e cần gấp :((
Giải giúp e bài 9,10,11 với aạ e cần gấp :((
