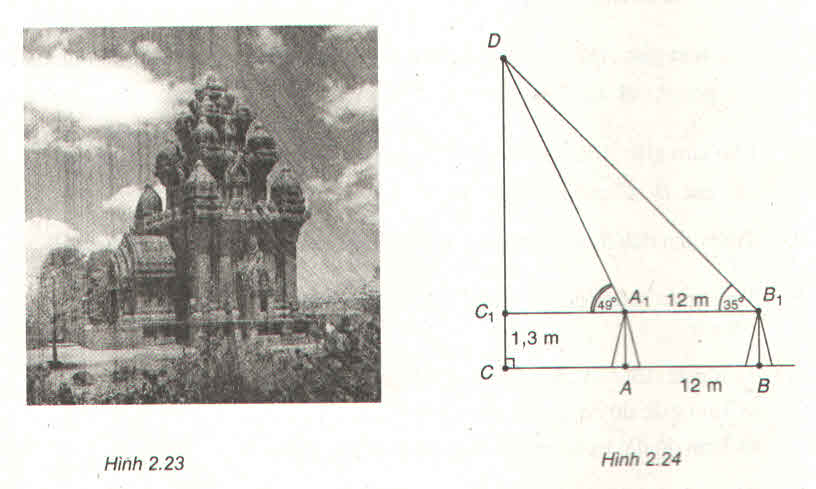
Giả sử chúng ta cần đo chiều cao CD của một cái tháp với C là chân tháp, D là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm A, B có khoảng cách AB = 30m sao cho 3 điểm A, B, C thẳng hàng người ta đo được các góc \(\widehat{CAD}=43^0;\widehat{CBD}=67^0\) (h.2.18). Hãy tính chiều cao CD của tháp ?
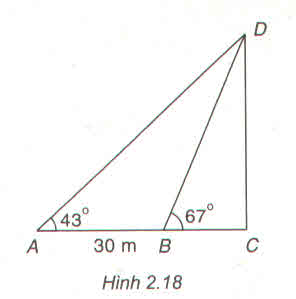
Có:
\(DC=AC.tan43^o=\left(AB+BC\right).tan43^o\).
\(DC=BC.tan67^o\).
Vì vây:
\(\left(AB+BC\right).tan43^o=BC.tan67^o\)
\(\Leftrightarrow BC=\dfrac{AB.tan43^o}{tan67^o-tan43^o}=26,55m\).
Suy ra: \(DC=BC.tan67^o=26,55.tan67^o=62,55m\).
Vậy chiều cao DC của chân tháp là 62,55m.