Question

Dựa vào đồ thị hàm số bậc hai \(y = f\left( x \right)\) trong mỗi Hình 30a, 30b, 30c, hãy viết tập nghiệm của mỗi bất phương trình sau: \(f\left( x \right) > 0;f\left( x \right) < 0;\)\(f\left( x \right) \ge 0;f\left( x \right) \le 0\).

Answer 1

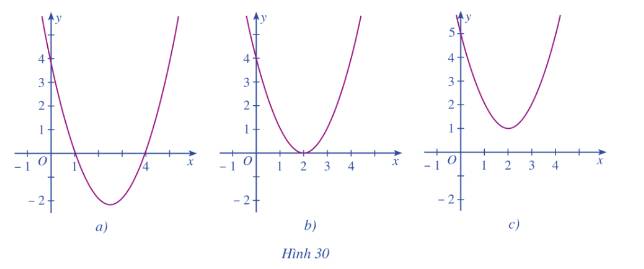
Hình 30a:

\(f\left( x \right) > 0\) có tập nghiệm là \(S = \left( { - \infty ;1} \right) \cup \left( {4; + \infty } \right)\)

\(f\left( x \right) < 0\) có tập nghiệm là \(S = \left( {1;4} \right)\)

\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \left( { - \infty ;1} \right] \cup \left[ {4; + \infty } \right)\)

\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left[ {1;4} \right]\)

Hình 30b:

\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\backslash \left\{ 2 \right\}\)

\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)

\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)

\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left\{ 2 \right\}\)

Hình 30c:

\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\)

\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)

\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)

\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \emptyset \)