Question

Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là một tam giác cân

Answer 1

Hướng dẫn:

Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên

AH ⊥ BC và HB = HC

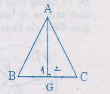
Xét hai tam giác vuông HAB và HAC có:

HB = HC

= 90⁰

AH: cạnh chung

Nên ∆HAB = ∆HAC => AB = AC

Vậy ∆ABC cân tại A

Answer 2

Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên

AH ⊥ BC và HB = HC

Xét hai tam giác vuông HAB và HAC có:

HB = HC

$\widehat{H_1}=\widehat{H_2}$ = 90⁰

AH: cạnh chung

Nên ∆HAB = ∆HAC => AB = AC

Vậy ∆ABC cân tại A

Answer 3

Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên

AH ⊥ BC và HB = HC

Xét hai tam giác vuông HAB và HAC có:

HB = HC

= 90⁰

AH: cạnh chung

Nên ∆HAB = ∆HAC => AB = AC

Vậy ∆ABC cân tại A

Answer 4

Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên

AH ⊥ BC và HB = HC

Xét hai tam giác vuông HAB và HAC có:

HB = HC

= 90⁰

AH: cạnh chung

Nên ∆HAB = ∆HAC => AB = AC

Vậy ∆ABC cân tại A