a) M nằm trong tam giác nên ABM
=> A, M, I không thẳng hang
Theo bất đẳng thức tam giác với ∆AMI:
AM < MI + IA (1)
Cộng vào hai vế của (1) với MB ta được:
AM + MB < MB + MI + IA
Mà MB + MI = IB
=> AM + MB < BI + IA
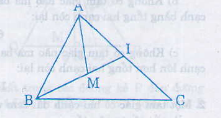
b) Ba điểm B, I, C không thẳng hang nên BI < IC + BC (2)
cộng vào hai vế của (2) với IA ta được:
BI + IA < IA + IC + BC
Mà IA + IC = AC
Hay BI + IA < AC + BC
c) Vì AM + MB < BI + IA
BI + IA < AC + BC
Nên MA + MB < CA + CB
Vậy số đo cạnh thứ ba là 11cm
Đúng 0
Bình luận (0)

