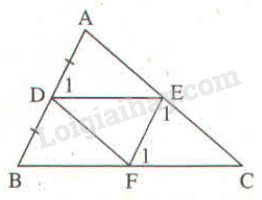
a) Vì \(EF\) // \(AB\left(gt\right)\)
=> \(EF\) // \(BD.\)
=> \(\widehat{EFD}=\widehat{BDF}\) (vì 2 góc so le trong).
+ Vì \(DE\) // \(BC\left(gt\right)\)
=> \(DE\) // \(FB.\)
=> \(\widehat{FDE}=\widehat{DFB}\) (vì 2 góc so le trong).
Xét 2 \(\Delta\) \(DBF\) và \(FED\) có:
\(\widehat{BDF}=\widehat{EFD}\left(cmt\right)\)
Cạnh DF chung
\(\widehat{DFB}=\widehat{FDE}\left(cmt\right)\)
=> \(\Delta DBF=\Delta FED\left(g-c-g\right)\)
=> \(BD=EF\) (2 cạnh tương ứng).
Mà \(AD=BD\) (vì D là trung điểm của \(AB\)).
=> \(AD=EF.\)
b) Vì \(DE\) // \(BC\left(gt\right)\)
=> \(\widehat{D_1}=\widehat{B}\) (vì 2 góc đồng vị) (1).
+ Vì \(EF\) // \(AB\left(gt\right)\)
=> \(\widehat{F_1}=\widehat{B}\) (vì 2 góc đồng vị) (2).
=> \(\widehat{E_1}=\widehat{A}\) (vì 2 góc đồng vị).
Từ (1) và (2) => \(\widehat{D_1}=\widehat{F_1}.\)
Xét 2 \(\Delta\) \(ADE\) và \(EFC\) có:
\(\widehat{A}=\widehat{E_1}\left(cmt\right)\)
\(AD=EF\left(cmt\right)\)
\(\widehat{D_1}=\widehat{F_1}\left(cmt\right)\)
=> \(\Delta ADE=\Delta EFC\left(g-c-g\right).\)
c) Theo câu b) ta có \(\Delta ADE=\Delta EFC.\)
=> \(AE=EC\) (2 cạnh tương ứng).
Chúc bạn học tốt!




