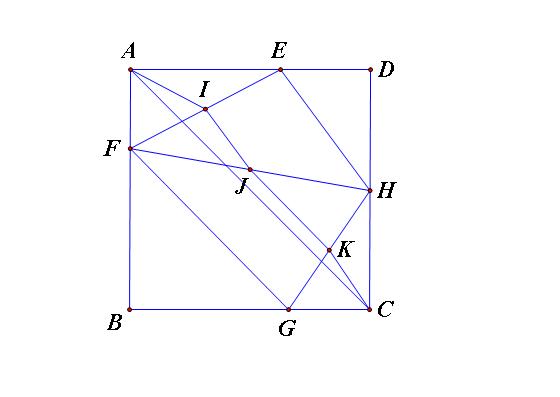
Gọi EFGH là tứ giác nội tiếp hình vuông
(\(E\in AB,F\in BC,G\in CD,H\in AD\)) , Từ E,F,G,H lần lượt dựng các đường thẳng vuông góc với BD tại P,Q,M,N; I và K là giao điểm của AG và EF.
Ta có : \(AI\ge AM=MP;GI\ge MP=GM;EK\ge EP=BP;KF\ge FQ=BK\)
\(\Rightarrow AG+EF=AI+IG+EK+KF\ge\left(PM+BQ\right)+\left(PN+BP\right)\)
Mặt khác, lại có : \(EH\ge NP;FG\ge MQ\)
\(\Rightarrow EF+FG+GH+HE\ge\left(PM+MQ+BQ\right)+\left(PN+NP+BP\right)\)
\(=BD+BD=2\)
\(\Rightarrow EF+FG+GH+GE\ge2\) (dpcm)
Ta có ( Áp dụng tính chất đường trung bình và trung tuyến ứng với cạnh huyền trong tam giác vuông)
Suy ra \(P_{EFGH}=2\left(AI+IJ+JK+KC\right)\ge2AC=2\)

Theo định lí Pytago ta có:
\(EH=\sqrt{AE^2+AH^2}\ge\frac{AE+AH}{\sqrt{2}}\)
Tương tự
\(EF\ge\frac{BE+BF}{\sqrt{2}}\)
\(FG\ge\frac{CF+CG}{\sqrt{2}}\)
\(HG\ge\frac{DG+HD}{\sqrt{2}}\)
Cộng từng vế ta được : \(EH+EF+FA+GH\ge\frac{AB+BC+CA+AD}{\sqrt{2}}=\frac{4AB}{\sqrt{2}}\)
Dễ chứng minh : \(AB=\frac{1}{\sqrt{2}}\rightarrow P_{EFGH}\ge\frac{4AB}{\sqrt{2}}=2\)
Dấu "=" xảy ra khi và chỉ khi E,F,G,H lần lượt là trung điểm các cạnh tương ứng

