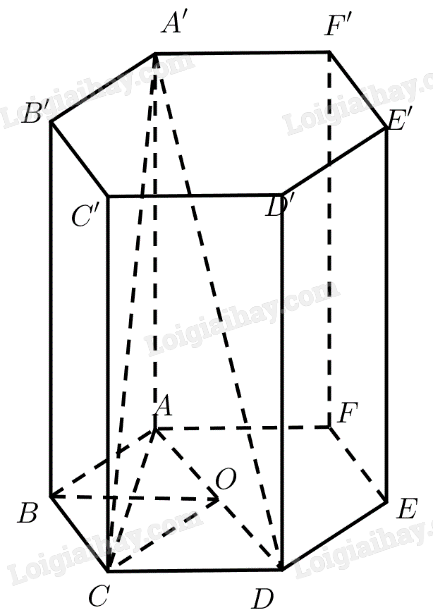
Tam giác \(ABC\) có:
\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}} = a\sqrt 3 \)
\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AC\)
\( \Rightarrow \Delta AA'C\) vuông tại \(A\)
\( \Rightarrow A'C = \sqrt {AA{'^2} + A{C^2}} = \sqrt {{h^2} + 3{{\rm{a}}^2}} \).
Gọi \(O\) là tâm lục giác đều \(ABC{\rm{DEF}}\).
\(\Delta OAB,\Delta OC{\rm{D}}\) đều \( \Rightarrow OA = O{\rm{D}} = AB = a \Rightarrow A{\rm{D}} = 2a\)
\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AD\)
\( \Rightarrow \Delta AA'D\) vuông tại \(A\)
\( \Rightarrow A'D = \sqrt {AA{'^2} + A{D^2}} = \sqrt {{h^2} + 4{{\rm{a}}^2}} \).