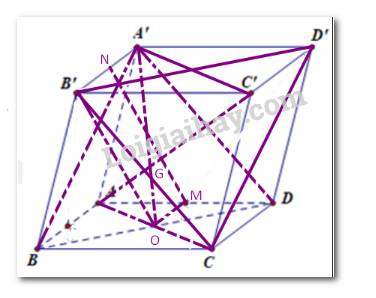
a) Ta có: (ABCD) // (A’B’C’D’)
\(\left( {B'D'DB} \right) \cap \left( {A'B'C'D'} \right) = B'D',\)
\(\left( {B'D'DB} \right) \cap \left( {ABCD} \right) = BD\).
Suy ra B'D' // DB.
Xét (A'BD) và (CB'D') có BD // B'D', A'B // CD'.
Suy ra (A'BD) //(CB'D').
Xét tứ giác B'NMO ta có: B'N = MO, B'N // MO.
Suy ra B'NMO là hình bình hành.
Suy ra B'O // MN hay MN // (BDD'B').
b) Xét tứ giác A'C'OA ta có: A'C' // AO, A'C' = 2AO
Suy ra A'G =2GO.
Mà O là trung điểm BD.
Suy ra G là trọng tâm tam giác A'BD.
Như vậy AC' đi qua trọng tâm G của tam giác A'BD.

