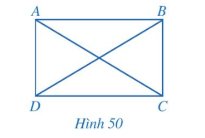
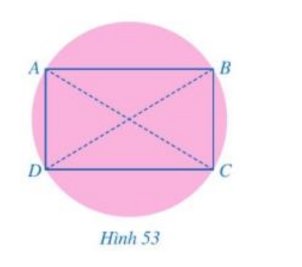
Do ABCD là hình chữ nhật, O là giao điểm của AC và BD
Suy ra OA = OB = OC = OD.
Xét tứ giác MBNO có:
\(\widehat M = \widehat N = {90^0}\) (Do M, N lần lượt là hình chiếu của O trên AB, BC)
\(\widehat B = {90^0}\)
nên MBNO là hình chữ nhật.
Suy ra MN = BO (tính chất hai đường chéo của hình chữ nhật)
\( MN = \dfrac{1}{2}AC\) (do \(BO = AO = OC = \dfrac{1}{2}AC\))