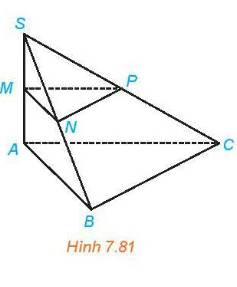
a) +) Xét tam giác SBC có
N, P lần lượt là trung điểm SB, SC
\( \Rightarrow \) PN là đường trung bình tam giác SBC
\( \Rightarrow \) PN // BC \( \Rightarrow \) PN // (ABC)
+) Xét tam giác SAB có
N, M lần lượt là trung điểm SB, SA
\( \Rightarrow \) MN là đường trung bình tam giác SAB
\( \Rightarrow \) MN // AB
+) \(\left. \begin{array}{l}PN//BC,MN//AB\\PN \cap MN = \left\{ N \right\},BC \cap AB = \left\{ B \right\}\end{array} \right\} \Rightarrow \left( {MNP} \right)//\left( {ABC} \right)\)
\( \Rightarrow \) d((MNP), (ABC)) = d(M, (ABC)) = MA \( = \frac{{SA}}{2} = \frac{h}{2}\) do SA \( \bot \) (ABC)
+) PN // (ABC) \( \Rightarrow \) d(NP,(ABC)) = d(N,(ABC)) = d(M,(ABC))\( = \frac{h}{2}\) (do MN // (ABC))
b)
Ta có \(SA \bot BC,AB \bot BC \Rightarrow BC \bot \left( {SAB} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SAB} \right) \bot \left( {SBC} \right)\)
\(\left( {SAB} \right) \cap \left( {SBC} \right) = SB\)
(SAB): kẻ \(AH \bot SB\)
\( \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow \) d(A,(SBC)) = AH
Xét tam giác SAB vuông tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{a^2}}} = \frac{{{a^2} + {h^2}}}{{{h^2}{a^2}}} \Rightarrow AH = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)