Cho hình chóp đều \(S.ABCD\) có các cạnh bên và các cạnh đáy đều bằng \(a\).
a) Chứng minh rằng các tam giác \(ASC\) và \(BSD\) là tam giác vuông cân.
b) Gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\), chứng minh rằng đường thẳng \(SO\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\).
c) Chứng minh rằng góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({45^ \circ }\).
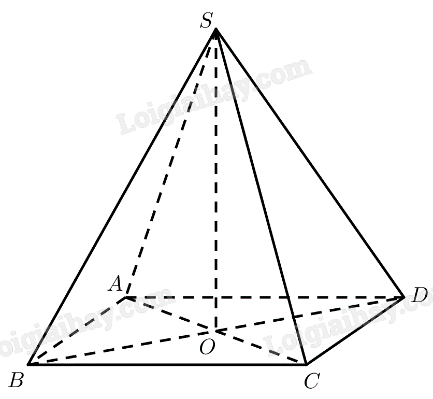
a) \(ABCD\) là hình vuông \( \Rightarrow AC = B{\rm{D}} = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
Xét \(\Delta ASC\) có: \(S{A^2} + S{C^2} = 2{a^2} = A{C^2},SA = SC\)
Vậy tam giác \(ASC\) là tam giác vuông cân tại \(S\).
Xét \(\Delta BSD\) có: \(S{B^2} + S{D^2} = 2{a^2} = B{{\rm{D}}^2},SB = SD\)
Vậy tam giác \(BSD\) là tam giác vuông cân tại \(S\).
b) \(\Delta ASC\) vuông cân tại \(S\) \( \Rightarrow SO \bot AC\)
\(\Delta BSD\) vuông cân tại \(S\) \( \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)
c) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)
\(\Delta ASC\) vuông cân tại \(S\) \( \Rightarrow \widehat {SAO} = {45^ \circ }\)
Vậy \(\left( {SA,\left( {ABCD} \right)} \right) = {45^ \circ }\).