Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
a) \(f'\left( x \right) = \left( {{x^3} - 3{x^2} + 2x + 1} \right)' = 3{x^2} - 6x + 2\)
\(f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 6x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3 - \sqrt 3 }}{3}\\x = \frac{{3 + \sqrt 3 }}{3}\end{array} \right.\)
Vậy \(x = \frac{{3 - \sqrt 3 }}{3},x = \frac{{3 + \sqrt 3 }}{3}\) thì \(f'\left( x \right) = 0\)
b) Bảng biến thiên:
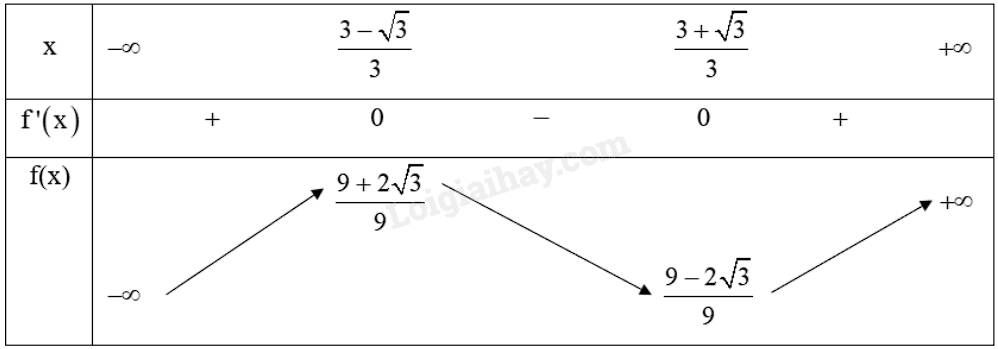
c) Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) đồng biến trên khoảng \(\left( { - \infty ;\frac{{3 - \sqrt 3 }}{3}} \right)\) và \(\left( {\frac{{3 + \sqrt 3 }}{3}; + \infty } \right)\).
Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) nghịch biến trên khoảng \(\left( {\frac{{3 - \sqrt 3 }}{3};\frac{{3 + \sqrt 3 }}{3}} \right)\).
