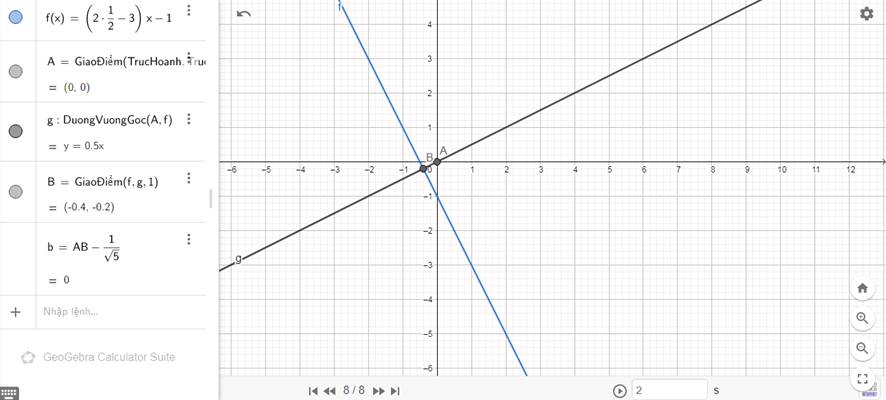
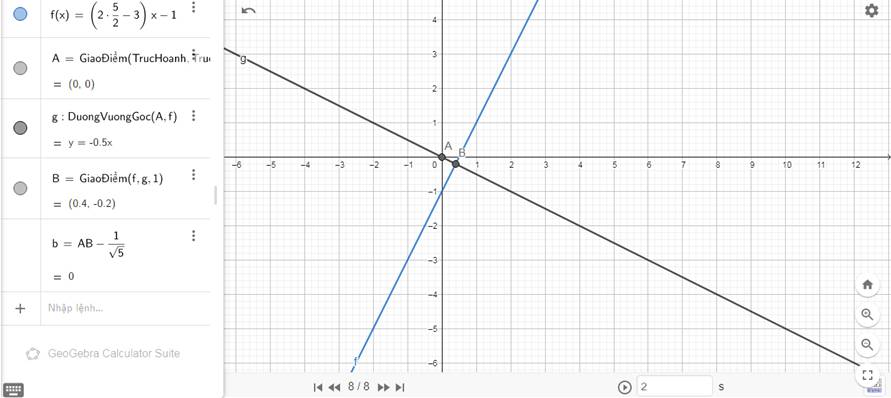
- Gọi M(x0,y0) ,N(x1,y1) lần lượt là giao điểm của đường thẳng (d): \(y=\left(2m-3\right)x-1\) với trục tung, trục hoành \(\Rightarrow x_0=y_1=0\).
Vì M(0;y0) thuộc (d) nên: \(y_0=\left(2m-3\right).0-1=-1\)
\(\Rightarrow M\left(0;-1\right)\) nên \(OM=1\) (đvđd)
\(N\left(x_1;0\right)\) thuộc (d) nên: \(\left(2m-3\right)x_1-1=0\Rightarrow x_1=\dfrac{1}{2m-3}\)
\(\Rightarrow N\left(\dfrac{1}{2m-3};0\right)\) nên \(ON=\dfrac{1}{2m-3}\) (đvđd)
*Hạ OH vuông góc với (d) tại H \(\Rightarrow OH=\dfrac{1}{\sqrt{5}}\)
Xét △OMN vuông tại O có OH là đường cao.
\(\Rightarrow\dfrac{1}{OM^2}+\dfrac{1}{ON^2}=\dfrac{1}{OH^2}\)
\(\Rightarrow1+\left(2m-3\right)^2=5\)
\(\Rightarrow2m-3=\pm2\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=\dfrac{1}{2}\end{matrix}\right.\) (nhận)