Question

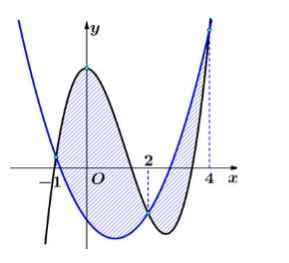
Cho hai hàm đa thức \(f\left(x\right)=ax^3+bx^2+cx+d\) và \(g\left(x\right)=mx^2+nx+p\). Biết rằng đồ thị hai hàm số \(y=f\left(x\right)\) và \(y=g\left(x\right)\) cắt nhau tại ba điểm có hoành độ \(-1;2;4\), đồng thời cắt trục tung tại \(M,N\) sao cho \(MN=6\) (tham khảo hình vẽ). Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho (phần gạch sọc) có diện tích bằng

A. \(\dfrac{125}{8}\)     B. \(\dfrac{253}{24}\)     C. \(\dfrac{253}{16}\)     D. \(\dfrac{253}{12}\)

Giải thích phần bôi vàng cho mình với ạ, mình cảm ơn nhiều♥

Answer 1

vì -1, 2, 4 là giao điểm của 2 đồ thị nên là nghiệm của pt f(x) - g(x)

f(x) và g(x) bậc cao nhất là bậc 3 nên viết được như trên