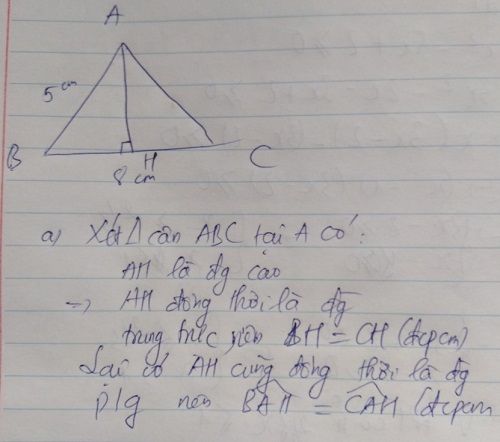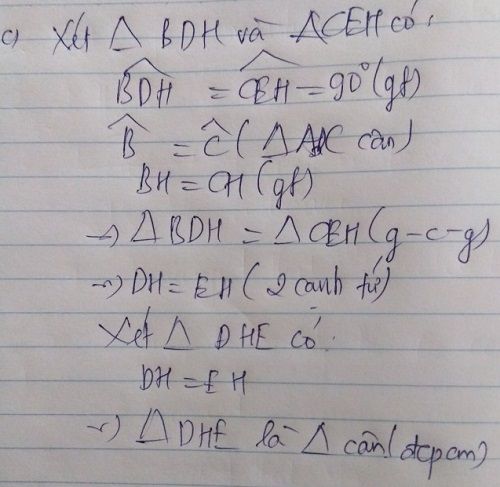làm giúp mik vs
Bài 1. Cho tam giác ABC cân có AB AC 5cm, BC 8cm. Kẻ AH vuông góc BC (H thuộc BC).
a) Chứng minh: HB HC và BHA CAH
b) Tính độ dài AH.
c) Kẻ HD vuông góc AB (D thuộc AB), kẻ HE vuông góc AC (E thuộc AC). Chứng minh: BD CE.
d) HE cắt AB tại G, DH cắt AC tại I. Chứng minh tam giác GHI cân.
e) Gọi M là trung điểm của GI. Chứng minh ba điểm A, H, M thẳng hàng.
Bài 2. Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. Trên BC lấy điểm M sao cho BM BA, trên AC lấy điểm N sa...
Đọc tiếp
làm giúp mik vs
Bài 1. Cho tam giác ABC cân có AB = AC = 5cm, BC = 8cm. Kẻ AH vuông góc BC (H thuộc BC).
a) Chứng minh: HB = HC và BHA = CAH
b) Tính độ dài AH.
c) Kẻ HD vuông góc AB (D thuộc AB), kẻ HE vuông góc AC (E thuộc AC). Chứng minh: BD = CE.
d) HE cắt AB tại G, DH cắt AC tại I. Chứng minh tam giác GHI cân.
e) Gọi M là trung điểm của GI. Chứng minh ba điểm A, H, M thẳng hàng.
Bài 2. Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC. Trên BC lấy điểm M sao cho BM = BA, trên AC lấy điểm N sao cho AN = AH. Chứng minh MN vuông góc AC.
Bài 3: Cho tam giác ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc với CA (tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC). Trên tia Cx lấy điểm D sao cho CD = AB. Chứng minh ba điểm B, M, D thẳng hàng.
Bài 4:Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm M, trên tia đối tia CA lấy điểm N sao cho BM = CN. Gọi K là trung điểm MN. Chứng minh ba điểm B, K, C thẳng hàng
Bài 5: Cho tam giác cân ABC, AB = AC. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB và AC lần lượt ở M và N. Chứng minh rằng:
a) DM = EN; b) Đường thẳng BC cắt MN tại điểm I là trung điểm của MN
c) Đường thẳng vuông góc với MN tại I luôn luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.
Bài 6: Cho tam giác đều ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Chứng minh DC vuông góc AC.
Bài 7: Cho tam giác ABC vuông tại C. Phân giác góc A và góc B cắt AC ở E, cắt BC ở D. Từ D, E hạ các đường vuông góc xuống AB cắt AB ở M và N. Tính góc MCN.