Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Chương II : Tam giác
Các câu hỏi tương tự
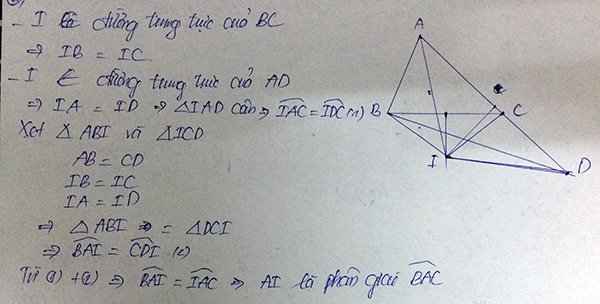
Bài 12: Cho tam giác ABC có AB AC. Trên tia đối của tia CA lấy điểm D sao cho CD AB. Gọi H, K lần lượt là trung điểm của AD, BC. Trung trực AD, BC cắt nhau tại I. Vẽ IE vuông góc với AB tại E.a) Chứng minh : IB IC; IA ID.b) Chứng minh: và AI là phân giác của góc BAC.c) Chứng minh: BE HC và AI là đường trung trực của đoạn thẳng EH.d) Từ C kẻ đường thẳng song song với AB, cắt đường thẳng EH tại F. Chứng minh: và E, K, F thẳng hàng.
Đọc tiếp
Bài 12: Cho tam giác ABC có AB < AC. Trên tia đối của tia CA lấy điểm D sao cho CD = AB. Gọi H, K lần lượt là trung điểm của AD, BC. Trung trực AD, BC cắt nhau tại I. Vẽ IE vuông góc với AB tại E.
a) Chứng minh : IB = IC; IA = ID.
b) Chứng minh: và AI là phân giác của góc BAC.
c) Chứng minh: BE = HC và AI là đường trung trực của đoạn thẳng EH.
d) Từ C kẻ đường thẳng song song với AB, cắt đường thẳng EH tại F. Chứng minh: và E, K, F thẳng hàng.
Cho ∆ABC có AB AC. Tia phân giác của góc A cắt BC tại D. Trên AC lấy điểm E sao cho AB AE. Gọi I là giao điểm của AD và BE. a) Chứng minh rằng: ∆AIB ∆AIE. b) Chứng minh: AD ⊥ BE. c) Vẽ IF là tia đối của tia IA sao cho IF IA. Chứng minh rằng: AB // EF. d) Qua A vẽ AH ⊥AB sao cho AH AB và vẽ AK⊥AC sao cho AK AC (H và K nằm khác phía đối với AD). Chứng minh rằng BK CH.
Đọc tiếp
Cho ∆ABC có AB < AC. Tia phân giác của góc A cắt BC tại D. Trên AC lấy điểm E sao cho AB = AE. Gọi I là giao điểm của AD và BE.
a) Chứng minh rằng: ∆AIB = ∆AIE.
b) Chứng minh: AD ⊥ BE.
c) Vẽ IF là tia đối của tia IA sao cho IF =IA. Chứng minh rằng: AB // EF.
d) Qua A vẽ AH ⊥AB sao cho AH = AB và vẽ AK⊥AC sao cho AK = AC (H và K nằm khác phía đối với AD). Chứng minh rằng BK = CH.
cho ΔABC cân tại A, tia phân giác của góc A cắt BC tại I. Lấy điểm M bất kì trên cạnh AI. Đường thẳng CM cắt AB tại D.
a, Chứng minh CM = BM
b, Chứng minh AI là đường trung trực của đoạn thẳng BC
c, Từ D kẻ DH ⊥ BC(H ϵ DC). Chứng minh góc BAC = góc BDH x 2
Cho tam giác ABC cân tại A, AM là phân giác góc A (M thuộc BC)
a/ chứng minh MB = MC
b/ Gọi I là trung điểm AC. Trên tia đối của tia đối của tia IB, lấy D sao cho BI = ID. Chứng minh AB // CD
c/ Gọi K là giao điểm của AM và CD. Chứng minh KC + IB + CD > AM + IA
Cho ΔABC vuông tại A, có AB = 9cm, BC = 15 cm, AC=12 cm.
a) so sánh các góc của ΔABC
b) trên tia đối của AB lấy điểm D sao cho A là trung điểm của đoạn thẳng BD. Chừng minh ΔABC = ΔADC
c) E là trung điểm cạnh CD,BE cắt AC ở I. Chứng minh DI đi qua trung điểm cạnh BC
cho tam giác ABC ( ABAC) , trên cạnh Bc lấy điểm E ( E không trùng với B và C ) . gọi I là trung điểm của Ae. đường thẳng đi qua và song song với BC cắt tia BI tại M
a/ chứng minh rằng ambe
b/ trên tia đối của tia IC lấy điểm N sao cho InIC . Chứng minh rằng AN // Ec và ba điểm M,A,N thẳng hàng
c/ Quá I kẻ đường thẳng vuông góc với NC , cắt đường thẳng Mn tại F . Chứng minh rằng Cn là tai phân giác của góc BCF
Đọc tiếp
cho tam giác ABC ( AB<AC) , trên cạnh Bc lấy điểm E ( E không trùng với B và C ) . gọi I là trung điểm của Ae. đường thẳng đi qua và song song với BC cắt tia BI tại M
a/ chứng minh rằng am=be
b/ trên tia đối của tia IC lấy điểm N sao cho In=IC . Chứng minh rằng AN // Ec và ba điểm M,A,N thẳng hàng
c/ Quá I kẻ đường thẳng vuông góc với NC , cắt đường thẳng Mn tại F . Chứng minh rằng Cn là tai phân giác của góc BCF
Cho tam giác ABC a) Cho biết góc A= 80 độ, góc B= 60 độ. So sánh các cạnh của tam giác ABC b) Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD. Chứng minh rằng: AB=CD và AB + AC > AD c) Gọi N là trung điểm của đoạn thẳng CD và K là giao điểm của AN và BC. Chứng minh rằng: BC = 3CK
cho tam giác ABC vuông tại A có góc B=góc2C
a. tính góc B, C:
b. gọi I là trung điểm của BC, trên tia đối của tia IA lấy điểm D sao cho ID=IA. chứng minh: AB=DC
c. chứng minh: DC vuông góc AC
ho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm K sao cho BK=BA. Gọi M là trung điểm của đoạn thẳng AK. a) Chứng minh: ∆AMB=∆KMB b) Đường thẳng BM cắt đường thẳng AC tại D. Chứng minh: DK vuông góc với BC. c) Trên tia đối của tia AB lấy điểm H sao cho ah=kc chứng minhh d k thẳng hàng