Ôn tập cuối năm phần số học
Các câu hỏi tương tự
Bài 5: Cho tổng 2 số bằng 2 và tích của chúng bằng 3. Hãy tìm tổng nghịch đảo của 2 số đó.
nhanh nha
Tính tổng nghịch đảo của các số sau: 3, 15, 35, 63, 99, 143
Bản thiết kế cho tầng một của ngôi nhà được xây trên một mảnh đất hình bình hành : a) Hãy tính diện tích của mảnh đất.b) Tính diện tích nền sân trước nhà; diện tích phòng khách; diện tích phòng bếp và phòng ăn của ngôi nhà.c) Để lát sàn phòng khách và phòng bếp người ta sử dụng lần lượt hai loại gỗ lát sàn với đơn giá 380000 đồng và 300000 đồng cho mỗi mét vuông sàn. Hãy tính số tiền cần chi trả cho việc lát gỗ.
Đọc tiếp
Bản thiết kế cho tầng một của ngôi nhà được xây trên một mảnh đất hình bình hành :
a) Hãy tính diện tích của mảnh đất.
b) Tính diện tích nền sân trước nhà; diện tích phòng khách; diện tích phòng bếp và phòng ăn của ngôi nhà.
c) Để lát sàn phòng khách và phòng bếp người ta sử dụng lần lượt hai loại gỗ lát sàn với đơn giá 380000 đồng và 300000 đồng cho mỗi mét vuông sàn. Hãy tính số tiền cần chi trả cho việc lát gỗ.
Hãy điền các từ thích hợp vào chỗ (.....) trong bảng so sánh cách tìm ƯCLN và BCNN của hai hay nhiều số :
Cách tìm
ƯCLN
BCNN
Phân tích các số ra thừa số nguyên tố
Xét các thừa số nguyên tố
...............
..............
Lập tích các thừa số đó, mỗi thừa số lấy với số mũ
...............
..............
Đọc tiếp
Hãy điền các từ thích hợp vào chỗ (.....) trong bảng so sánh cách tìm ƯCLN và BCNN của hai hay nhiều số :
| Cách tìm | ƯCLN | BCNN |
| Phân tích các số ra thừa số nguyên tố | ||
| Xét các thừa số nguyên tố | ............... | .............. |
| Lập tích các thừa số đó, mỗi thừa số lấy với số mũ | ............... | .............. |
cho 2022 số nguyên phân biệt , trong đó tích của ba số bất kỳ luôn là số nguyên âm. Chứng tỏ rằng tích của 2022 số nguyên đó là một số nguyên dương ? cứu tui với*
Tỉ số vàng
Người Cổ Hy Lạp và người Cổ Ai Cập đã ý thức được những tỉ số đẹp trong các công trình xây dựng. Họ cho rằng hình chữ nhật đẹp là hình chữ nhật có tỉ số giữa chiều dài và chiều rộng là 1:0,618 (các hình chữ nhật : DPLC, APLB,HGLB,.....trong hình 17). Vì thế, tỉ số này được gọi là tỉ số vàng (theo cách gọi của nhà danh họa và nhà khoa học người Ý nổi tiếng Lê - ô - nác - đô đa Vin - xi)
Khi nghiên cứu kiến trúc của Đền cổ Pác - tê - nông (h.18) ở A - ten (Hy Lạp), người ta nhận xét...
Đọc tiếp
"Tỉ số vàng"
Người Cổ Hy Lạp và người Cổ Ai Cập đã ý thức được những tỉ số "đẹp" trong các công trình xây dựng. Họ cho rằng hình chữ nhật đẹp là hình chữ nhật có tỉ số giữa chiều dài và chiều rộng là \(1:0,618\) (các hình chữ nhật : DPLC, APLB,HGLB,.....trong hình 17). Vì thế, tỉ số này được gọi là "tỉ số vàng" (theo cách gọi của nhà danh họa và nhà khoa học người Ý nổi tiếng Lê - ô - nác - đô đa Vin - xi)
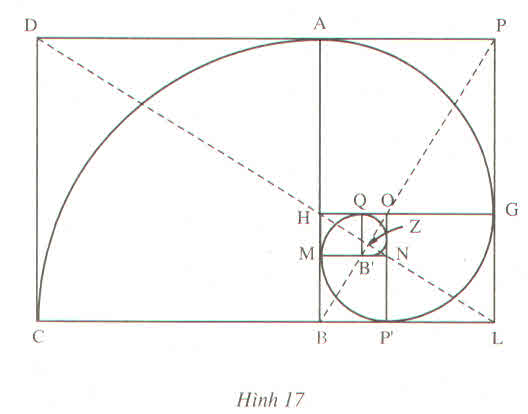
Khi nghiên cứu kiến trúc của Đền cổ Pác - tê - nông (h.18) ở A - ten (Hy Lạp), người ta nhận xét kích thước của các hình hình học trong đền phần lớn chịu ảnh hưởng của "tỉ số vàng"
a) Các kích thước của một hình chữ nhật tuân theo "tỉ số vàng", biết rằng chiều rộng của nó đo được 3,09m. Tính chiều dài của hình chữ nhật đó ?
b) Chiều dài của một hình chữ nhật là 4,5m. Để có "tỉ số vàng" thì chiều rộng của nó là bao nhiêu ?
c) Một khu vườn hình chữ nhật có chiều dài là 15,4m, chiều rộng là 8m. Khu vườn này có đạt "tỉ số vàng" không ?

Bài 1. (3 điểm) Cho biểu thức ![]() .
.
a. Tìm các số nguyên x để biểu thứ A là phân số.
Tìm các số nguyên x để A là một số nguyên
Bài 1. (3 điểm) Cho biểu thức .
a. Tìm các số nguyên x để biểu thứ A là phân số.
b. Tìm các số nguyên x để A là một số nguyên
Tìm giao của tập hợp C các số chẵn và tâp hợp L các số lẻ
