a) Vẽ các đường thẳng \(x + 2y = - 4\)(nét đứt) và \(y = x + 5\) (nét liền)
Thay tọa độ O vào \(x + 2y < - 4\) ta được: \(0 + 2.0 < - 4\) (Sai)
=> Gạch đi phần chứa O.
Thay tọa độ O vào \(y \ge x + 5\) ta được: \(0 \ge 0 + 5\) (Sai)
=> Gạch đi phần chứa O.
\(x + 2y = -4 => y = \frac{-4 - x}{2} \)
Xét phương trình hoành độ giao điểm của hai đường thẳng \(x + 2y = - 4\) và \(y = x + 5\), ta được:
\( \frac{-4 - x}{2} = x + 5 \\ x = \frac{-14}{3} \\ => y = \frac{1}{3} \)
Miền nghiệm của hệ:
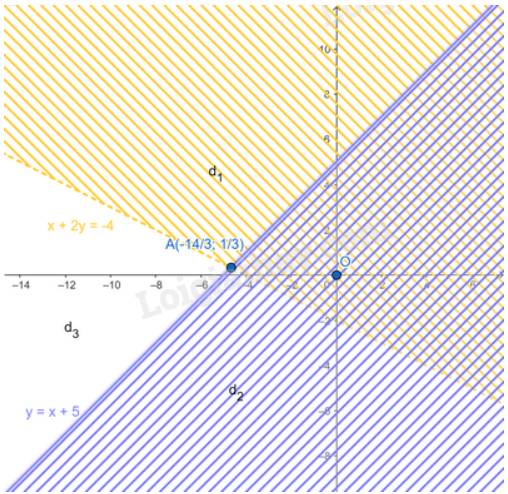
Từ hình vẽ ta thấy miền nghiệm của hệ là \(d_3\)
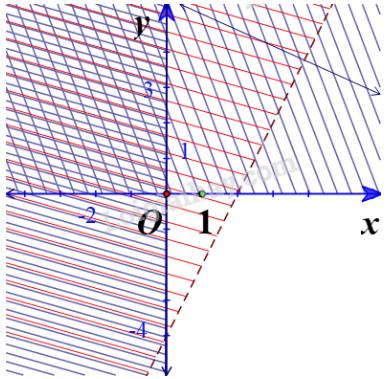
b) Vẽ các đường thẳng \(4x - 2y = 8\)(nét đứt) và hai trục (nét liền)
Thay tọa độ O vào \(4x - 2y > 8\) ta được: \(4.0 - 2.0 > 8\) (Sai)
=> Gạch đi phần chứa O.
Với \(x \ge 0\) thì gạch phần bên trái Oy
Với \(y \le 0\) thì gạch bên trên Ox
Miền nghiệm của hệ: