Question

Bài 1. Cho hình bình hành ABCD. Tia phân giác của góc A.cắt cạnh CD tại M. Tia phân giác của góc C cắt cạnh  AB tại N. Chứng minh

A) tứ giác AMCN là hình bình hành

B) 3 đường thẳng AC ,MN, BD đồng quy

Bài 2. Cho tứ giác ABCD. R là trung điểm AB. F là trung điểm CD. Gọi M, N, P, Q theo thứ tự là trung điểm của  À, CE, BF, DE. Chứng minh tứ giác MNPQ.là hình bình hành

Bài 3. Tìm x

(X+1)^3 - (x-1)^3 - 6x(x-1)^2 = -10 

Help me

Answer 1

1.a) Ta có : góc MAN= GÓC MCN \(\Rightarrow\)NC // AM (1)
Lại có ABCD là hình bình hành \(\Rightarrow\) AB//=DC (2)
từ (1) và (2) \(\Rightarrow\) ANCM là hình bình hành( tứ giác có 2 cặp cạnh // với nhau)

Answer 2

2)

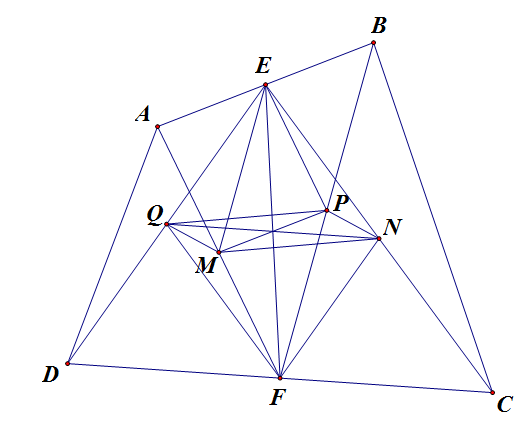
Sử dụng tính chất đường trung bình. Dễ dàng chứng minh $QENF,MEPF$ là hình bình hành
Vậy $EF$ và $QN$ giao nhau tại trung điểm mỗi đường, $EF$ và $MP$ giao nhau tại trung điểm mỗi đường.
$\Rightarrow QN$ giao $MP$ tại trung điểm mỗi đường.
Vậy $QPNM$ là hình bình hành. 

Answer 3

3)\(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^3+12x^2-6x+10=0\)

\(\Leftrightarrow-6x^3+18x^2-6x+12=0\)

\(\Leftrightarrow-6\left(x^3-3x^2+x-2\right)=0\)

hình như sai đề bn à