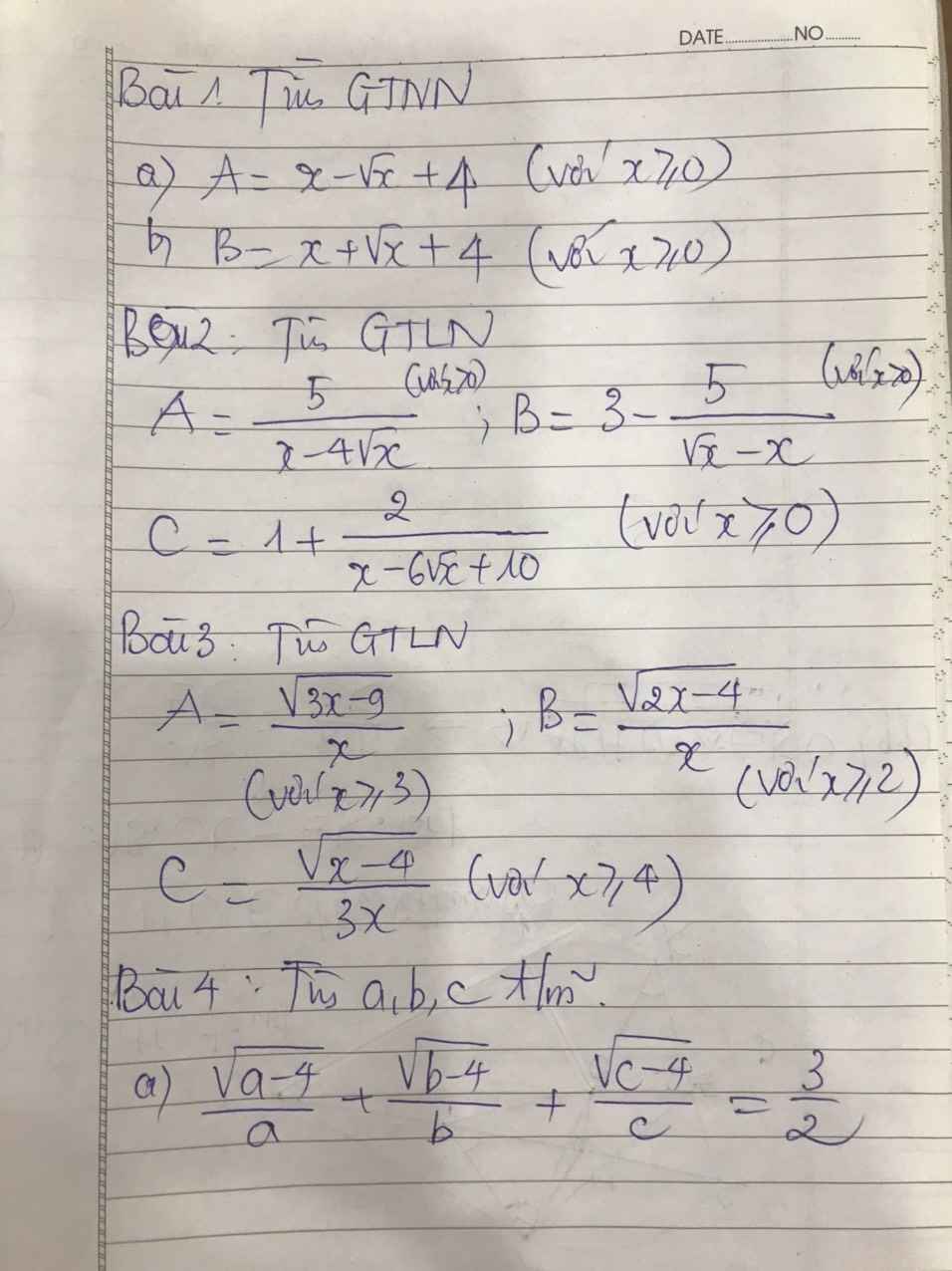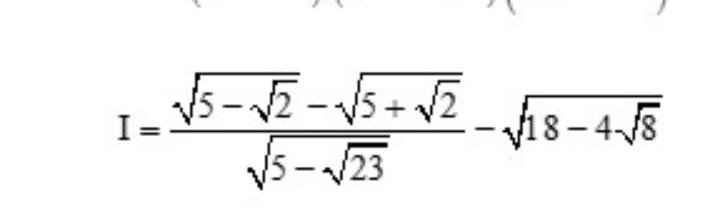a.ĐK x ≠ 1
Ta có: P= \(\dfrac{4}{\sqrt{x}+1}-\dfrac{2}{\sqrt{x}-1}-\dfrac{\sqrt{x}-7}{x-1}\)
= \(\dfrac{4.(\sqrt{x}-1)}{(\sqrt{x}+1)(\sqrt{x}-1)}-\dfrac{2.(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}\) \(-\dfrac{\sqrt{x}-7}{(\sqrt{x}+1)(\sqrt{x}-1)}\)
= \(\dfrac{4\sqrt{x}-4-2\sqrt{x}+2-\sqrt{x}+7}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
= \(\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
= \(\dfrac{1}{\sqrt{x}+1}\)
Vậy P = \(\dfrac{1}{\sqrt{x}+1}\)
b. Ta có: P ≤ -2
⇌ \(\dfrac{1}{\sqrt{x}+1}\le-2\)
⇌\(\dfrac{1}{\sqrt{x}+1}\)+2 ≤ 0
⇌ \(\dfrac{1+2\sqrt{x}+2}{\sqrt{x}+1}\le0\)
⇌\(\dfrac{2\sqrt{x}+3}{\sqrt{x}+1}\le0\)
⇌\(\left[{}\begin{matrix}\left\{{}\begin{matrix}2\sqrt{x}+3\ge0\\\sqrt{x}+1>0\end{matrix}\right.\\\left\{{}\begin{matrix}2\sqrt{x}+3\le0\\\sqrt{x}+1< 0\end{matrix}\right.\end{matrix}\right.\)⇌\(\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}\ge-\dfrac{3}{2}\\\sqrt{x}>-1\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}\le-\dfrac{3}{2}\\\sqrt{x}< -1\end{matrix}\right.\end{matrix}\right.\)⇌\(\left[{}\begin{matrix}x>-1\\x\le-\dfrac{3}{2}\end{matrix}\right.\)
Vậy với x>-1 hoặc \(x\le-\dfrac{3}{2}\) thì P ≤ -2
P= 4/\(P=\dfrac{4}{\sqrt{X}+1}-\dfrac{2}{\sqrt{X}-1}-\dfrac{\sqrt{X}-7}{x-1}a,RutgonPb,xacdinhxdePnhohonhoacbang-2\)


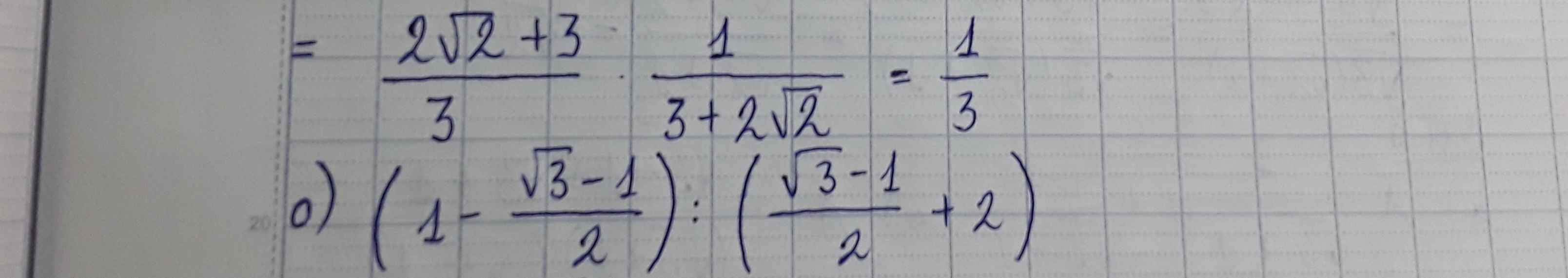 giải giúp mk câu o vs ạ
giải giúp mk câu o vs ạ