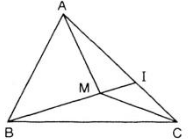
1. Cho △ABC, M là điểm nằm trong △ABC. Gọi I là giao điểm của BM và AC. Chứng minh rằng:
a) MA + MB < IA + IB
b) MA + MB < AC + BC
2. Cho 2 điểm A, B nằm ngoài đường thẳng d và cùng nằm trên nửa mặt phẳng bờ d. Xác định vị trí điểm M trên đường thẳng d để AM + BM nhỏ nhất.
3. Cho △ABC (AB > AC). Tia phân giác của \(\widehat{BAC}\) cắt BC tại D. M là điểm nằm trên đoạn thẳng AD. Chứng minh rằng MB - MC < AB - AC
Bài 2. Lời giải:
- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M. M chính là điểm cần tìm.
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA=MA’. Do đó : MA+MB=MA’+MB=A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A+M’B=M’A’+M’B lớn hơn hoặc bằng A'B. Dấu bằng chỉ xảy ra khi A’M’B thẳng hàng. Nghĩa là M trùng với M’
Bài 1:
a) Vì M là điểm nằm trong \(\Delta ABC\left(gt\right)\)
=> 3 điểm \(A,M,I\) không thẳng hàng.
+ Xét \(\Delta AMI\) có:
\(MA< MI+IA\) (theo bất đẳng thức trong tam giác) (1).
Cộng \(MB\) vào hai vế của (1) ta được:
\(MA+MB< MB+MI+IA\)
Mà \(MB+MI=IB\left(gt\right)\)
=> \(MA+MB< IB+IA.\)
Hay \(MA+MB< IA+IB\left(đpcm1\right).\)
b) Vì I là giao điểm của \(BM\) và \(AC\left(gt\right)\)
=> 3 điểm \(B,I,C\) không thẳng hàng.
+ Xét \(\Delta BIC\) có:
\(IB< IC+BC\) (theo bất đẳng thức trong tam giác) (2).
Cộng \(IA\) vào hai vế của (2) ta được:
\(IA+IB< IA+IC+BC\)
Mà \(IA+IC=AC\left(gt\right)\)
=> \(IA+IB< AC+BC.\)
Mà \(MA+MB< IA+IB\left(cmt\right)\)
=> \(MA+MB< AC+BC\left(đpcm2\right).\)
Chúc bạn học tốt!
Bài 3:

Trên tia AB lấy điểm E sao cho \(AE=AC.\)
Mà \(AB>AC\left(gt\right)\)
=> E nằm giữa hai điểm A và B.
=> \(AE+BE=AB.\)
=> \(BE=AB-AE\)
Mà \(AE=AC\) (do cách vẽ).
=> \(BE=AB-AC\) (1).
+ Vì \(AD\) là tia phân giác của \(\widehat{BAC}\left(gt\right)\)
Mà \(M\in AD\left(gt\right)\)
=> \(AM\) là tia phân giác của \(\widehat{BAC}.\)
+ Xét 2 \(\Delta\) \(AEM\) và \(ACM\) có:
\(AE=AC\) (do cách vẽ)
\(\widehat{EAM}=\widehat{CAM}\) (vì \(AM\) là tia phân giác của \(\widehat{BAC}\))
Cạnh AM chung
=> \(\Delta AEM=\Delta ACM\left(c-g-c\right)\)
=> \(ME=MC\) (2 cạnh tương ứng) (2).
+ Xét \(\Delta BEM\) có:
\(MB-ME< BE\) (theo bất đẳng thức trong tam giác) (3).
Từ (1), (2) và (3) => \(MB-MC< AB-AC\left(đpcm\right).\)
Chúc bạn học tốt!