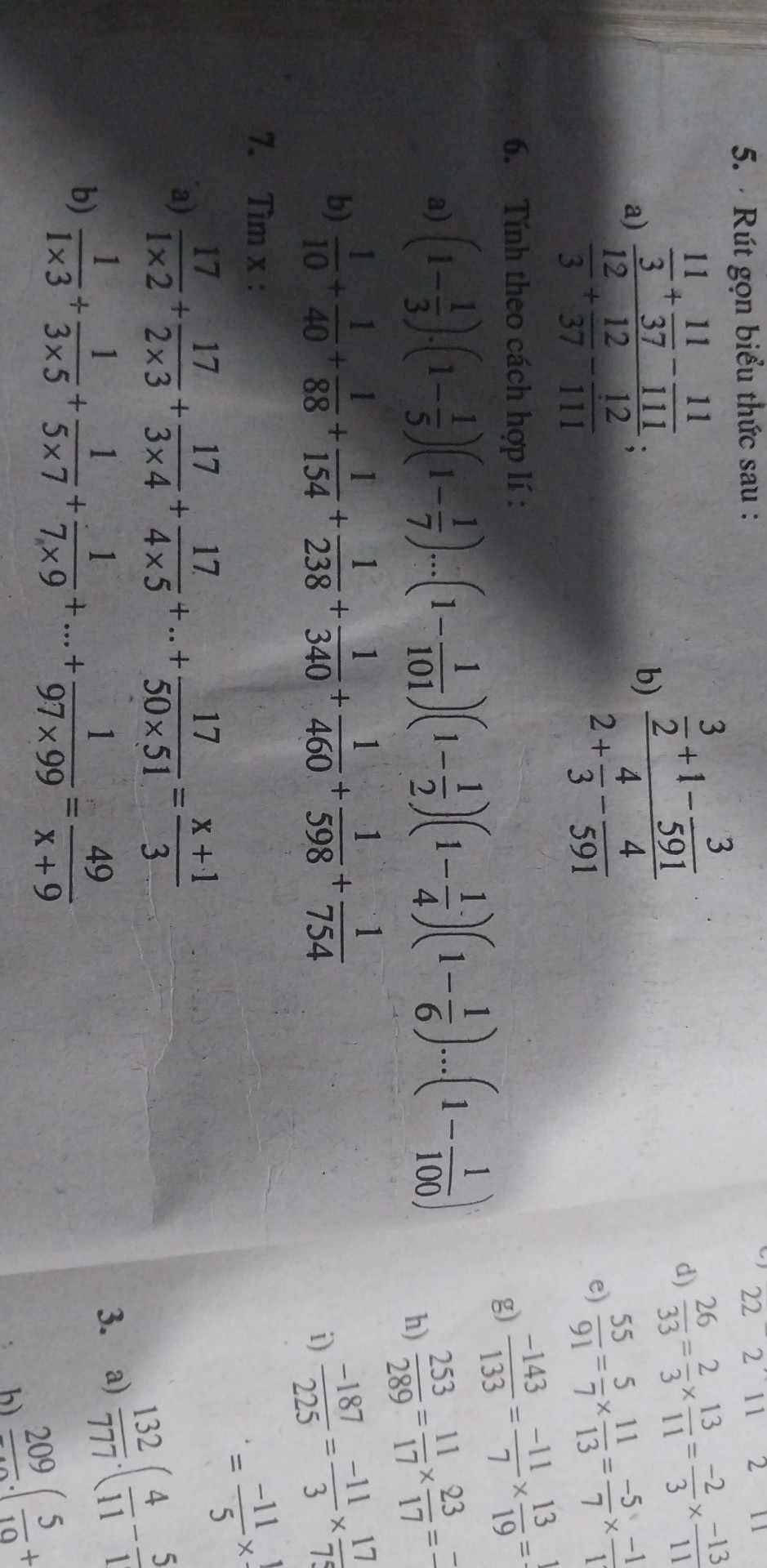5:
a: \(\dfrac{\dfrac{11}{3}+\dfrac{11}{37}-\dfrac{11}{111}}{\dfrac{12}{3}+\dfrac{12}{37}-\dfrac{12}{111}}\)
\(=\dfrac{11\left(\dfrac{1}{3}+\dfrac{1}{37}-\dfrac{1}{111}\right)}{12\left(\dfrac{1}{3}+\dfrac{1}{37}-\dfrac{1}{111}\right)}\)
\(=\dfrac{11}{12}\)
b: \(\dfrac{\dfrac{3}{2}+1-\dfrac{3}{591}}{2+\dfrac{4}{3}-\dfrac{4}{591}}\)
\(=\dfrac{\dfrac{3}{2}+\dfrac{3}{3}-\dfrac{3}{591}}{\dfrac{4}{2}+\dfrac{4}{3}-\dfrac{4}{591}}\)
\(=\dfrac{3\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{591}\right)}{4\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{591}\right)}=\dfrac{3}{4}\)
7:
a: \(\dfrac{17}{1\cdot2}+\dfrac{17}{2\cdot3}+...+\dfrac{17}{50\cdot51}=\dfrac{x+1}{3}\)
=>\(\dfrac{x+1}{3}=17\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{50\cdot51}\right)\)
=>\(x+1=51\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{50}-\dfrac{1}{51}\right)\)
=>\(x+1=51\cdot\dfrac{50}{51}=50\)
=>x=50-1=49
b: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{97\cdot99}=\dfrac{49}{x+9}\)
=>\(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{97\cdot99}=\dfrac{98}{x+9}\)
=>\(\dfrac{98}{x+9}=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}=1-\dfrac{1}{99}=\dfrac{98}{99}\)
=>x+9=99
=>x=90