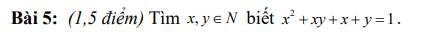\(x^2+xy+x+y=1\)
\(\Rightarrow x\left(x+y\right)+\left(x+y\right)=1\)
\(\Rightarrow\left(x+1\right)\left(x+y\right)=1\)
Nhưng x,y ϵ N nên:
\(x+1=1\)
\(\Rightarrow x=1-1\)
\(\Rightarrow x=0\)
\(x+y=1\)
\(\Rightarrow0+y=1\)
\(\Rightarrow y=1\)
Vậy: ...
\(x^2+xy+x+y=1\) \(\left(x;y\in N\right)\)
\(\Rightarrow x\left(x+y\right)+\left(x+y\right)=1\)
\(\Rightarrow\left(x+1\right)\left(x+y\right)=1\)
\(\Rightarrow\left(x+1\right);\left(x+y\right)\in U\left(1\right)=\left\{1\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(0;1\right)\right\}\)