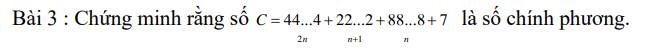Lời giải:
Đặt \(\underbrace{11....1}_{n}=a\Rightarrow 9a+1=10^n\)
\(C=4(\underbrace{11...1}_{n}.10^n+\underbrace{11...1}_{n})+2(\underbrace{111....1}_{n}.10+1)+8.\underbrace{111....1}_{n}+7\)
\(=4(a.10^n+a)+2(a.10+1)+8a+7\)
\(=4a(9a+1)+4a+20a+8a+9=36a^2+36a+9=(6a+3)^2\)
Vậy $C$ là scp
Thu gọn biểu thức đại số ta được A. -10x3y3 B. x3y3 C. 50x3y3 D. 0
Tìm x biết
1, \(\dfrac{-1}{4}-\dfrac{3}{4}:x=-\dfrac{11}{36}\)
2,\(\dfrac{3}{4}x-\dfrac{1}{2}=\dfrac{3}{7}\)
Tìm x biết
\(3\dfrac{1}{2}:0,4=x:1\dfrac{1}{7}\)
Tìm các số x, y, z biết rằng :
a. \(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}\)và x + y - z = 38
b. 7x = 10y = 12z và x + y + z = 685
tìm x 2x-3=x+1/2
a, x : y : z = 3 : 4 : 5 và 5z^2 - 3x^2 - 2y^2 = 594
giúp mik vs mik đang gấp , bn nào trả lời chi tiết và nhanh nhất thì mik sẽ tik cho nhs
cho đa thức
A =16x4-8x3y+7x2y2-9x4 ; B= -15x4+3x3y-5x2y2-6y4 ; C = 5x3y+3x2y2+17y4+1
chứng minh một trong ba đa thức này có giá trị dương với mọi x, y
