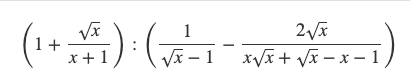\(\Leftrightarrow\left(\dfrac{x+1}{x+1}+\dfrac{\sqrt{x}}{x+1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{\sqrt{x}\left(x+1\right)-\left(x+1\right)}\right)\)
\(\Leftrightarrow\left(\dfrac{x+1+\sqrt{x}}{x+1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-1\right)\left(x+1+\sqrt{x}\right)}{\left(x+1\right)\left(\sqrt{x}-1\right)}:\left(\dfrac{x+1}{\left(x+1\right)\left(\sqrt{x}-1\right)}-\dfrac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\left(x+1\right)\left(\sqrt{x}-1\right)}:\dfrac{x-2\sqrt{x}+1}{\left(x+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\left(x+1\right)\left(\sqrt{x}-1\right)}:\dfrac{\left(\sqrt{x}-1\right)^2}{\left(x+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\left(x+1\right)\left(\sqrt{x}-1\right)}:\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{\left(x+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\left(x+1\right)\left(\sqrt{x}-1\right)}{\left(x+1\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow\dfrac{x+\sqrt{x}+1}{\sqrt{x}-1}\)
đk : x>= 0; x khác 1
\(=\left(\dfrac{x+1+\sqrt{x}}{x+1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{\sqrt{x}\left(x+1\right)-\left(x+1\right)}\right)\)
\(=\dfrac{x+1+\sqrt{x}}{x+1}:\left(\dfrac{x+1-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+1\right)}\right)=\dfrac{x+\sqrt{x}+1}{x+1}:\dfrac{\sqrt{x}-1}{x+1}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}-1}\)