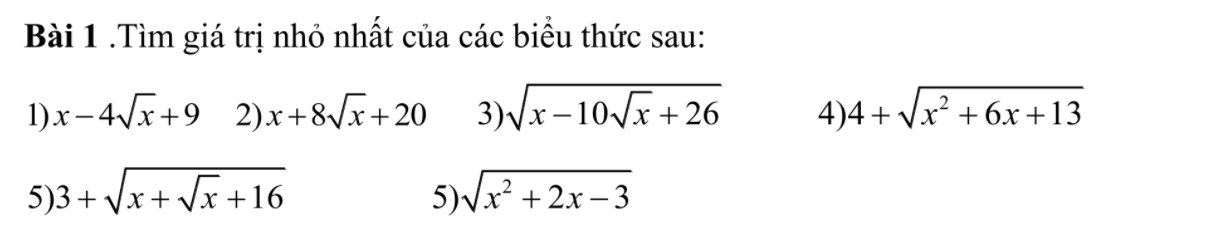2. ĐKXĐ: $x\geq 0$
Với $x\geq 0$ thì $x+8\sqrt{x}+20\geq 0+8.0+20=20$
Vậy GTNN của biểu thức là $8$ khi $x=0$
5. ĐKXĐ: $x\geq 0$
Với mọi $x\geq 0$ thì $3+\sqrt{x+\sqrt{x}+16}\geq 3+\sqrt{0+0+16}=7$
Vậy GTNN của biểu thức là $7$ khi $x=0$
1.
$x-4\sqrt{x}+9=(x-4\sqrt{x}+4)+5=(\sqrt{x}-2)^2+5\geq 5$
Vậy GTNN của biểu thức là $5$ tại $\sqrt{x}-2=0\Leftrightarrow x=4$
3.
$\sqrt{x-10\sqrt{x}+26}=\sqrt{(\sqrt{x}-5)^2+1}\geq \sqrt{1}=1$
Vậy GTNN của biểu thức là $1$ tại $\sqrt{x}-5=0\Leftrightarrow x=25$
4.
$4+\sqrt{x^2+6x+13}=4+\sqrt{(x+3)^2+4}\geq 4+\sqrt{0+4}=6$
Vậy GTNN của biểu thức là $6$ khi $x+3=0\Leftrightarrow x=-3$
6.
$\sqrt{x^2+2x-3}\geq 0$ theo tính chất căn bậc 2 số học
Vậy GTNN của biểu thức là $0$. Giá trị này đạt tại $x^2+2x-3=0$
$\Leftrightarrow (x-1)(x+3)=0\Leftrightarrow x=1$ hoặc $x=-3$