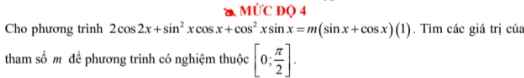Đặt \(cosx-sinx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)
\(2cos2x+sin^2x.cosx+cos^2x.sinx=m\left(sinx+cosx\right)\)
\(\Leftrightarrow2\left(cosx-sinx\right)\left(cosx+sinx\right)+sinx.cosx\left(cosx+sinx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left(cosx+sinx\right)\left(2cosx-2sinx+sinx.cosx-m\right)=0\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)\left[-\dfrac{1}{2}\left(cosx-sinx\right)^2+2\left(cosx-sinx\right)+1-m\right]=0\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)\left[-\dfrac{1}{2}t^2+2t+1-m\right]=0\)
Phương trình đã cho có nghiệm thuộc \(\left[0;\dfrac{\pi}{2}\right]\) khi phương trình \(m=f\left(t\right)=-\dfrac{1}{2}t^2+2t+1\) có nghiệm thuộc \(\left[-1;1\right]\).
\(\Leftrightarrow minf\left(t\right)\le m\le maxf\left(t\right)\)
\(\Leftrightarrow-\dfrac{3}{2}\le m\le3\)
P/s: Không biết đúng không nữa.
Lần sau đừng đăng nhiều lần, thấy người ta không làm tức là không làm được hoặc lười làm.
Đăng mấy lần cũng vậy thôi.
Đây mình làm xong lần sau rút kinh nghiệm.