`2^{2}.16>=2^{x}>4^{2}`
`->2^{2}.2^{4}>=2^{x}>(2^{2})^{2}`
`->2^{6}>=2^{x}>2^{4}`
`->6>=x>4`
Đúng 1
Bình luận (0)
\(2^2.16\ge2^x>4^2\)
\(2^2.2^4\ge2^x>\left(2^2\right)^2\)
\(2^6\ge2^x>2^4\Rightarrow x\in\left\{6;5\right\}\)
Đúng 1
Bình luận (0)
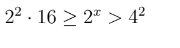
22. 24 ≥ 2x > 24
26 ≥ 2x > 24
=> 6 ≥ x > 4
=> x = { 5 ; 6 }
Đúng 0
Bình luận (0)
\(2^2.16\ge2^x>4^2\)
\(\rightarrow2^2.2^4\ge2^x>4^2\)
\(\rightarrow2^6\ge2^x>4^2\)
\(\rightarrow2^6\ge2^x>\left(2^2\right)^2\)
\(\rightarrow2^6\ge2^x>2^4\)
\(\Rightarrow6\ge x>4\)
\(\Rightarrow x=\left\{6;5\right\}\)
Đúng 1
Bình luận (0)
Ta có: \(2^2\cdot16\ge2^x>4^2\)
\(\Leftrightarrow2^6\ge2^x>2^4\)
hay \(x\in\left\{5;6\right\}\)
Đúng 0
Bình luận (0)




